题目内容
20.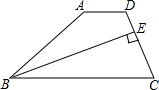 如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )| A. | $\frac{7}{4}$ | B. | $\frac{5}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
分析 延长BA,CD交于点F,显然△BEF≌△BEC,可知S△BCF=2S△BEC=4,根据AD∥BC知△ADF∽△BCF且相似比为1:4,根据相似三角形性质可得S△ADF,将S△BEF-S△ADF可得.
解答 解:延长BA,CD交于点F,
∵BE平分∠ABC,
∴∠EBF=∠EBC,
∵BE⊥CD,
∴∠BEF=∠BEC=90°,
在△BEF和△BEC中,
∵$\left\{\begin{array}{l}{∠EBF=∠EBC}\\{BE=BE}\\{∠BEF=∠BEC}\end{array}\right.$,
∴△BEF≌△BEC(ASA),
∴EC=EF,S△BEF=S△BEC=2,
∴S△BCF=S△BEF+S△BEC=4,
∵$\frac{CE}{DE}$=2,
∴$\frac{DF}{FC}$=$\frac{1}{4}$,
∵AD∥BC,
∴△ADF∽△BCF,
∴$\frac{{S}_{△ADF}}{{S}_{△BCF}}$=($\frac{DF}{CF}$)2=$\frac{1}{16}$
∴S△ADF=$\frac{1}{16}$×4=$\frac{1}{4}$,
∴S四边形ABCD=S△BEF-S△ADF=2-$\frac{1}{4}$=$\frac{7}{4}$.
故选:A.
点评 本题主要考查相似三角形的判定与性质,构建相似三角形利用相似三角形的性质来求面积是解决本题的关键.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (-2a2)3=8a6 | C. | 2a2+a2=3a2 | D. | a3÷a=a3 |
11.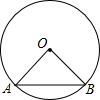 如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )
如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )
 如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )
如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )| A. | 4 | B. | 2 | C. | $2\sqrt{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
10.小明从家出发,先向东走350m到小亮家,然后它们又向南走500m到老师家,如果以老师家的位置为平面直角坐标系的坐标原点,正东方向为x轴正方向为x轴正方向,正北方向为y轴正方向,那么小明家的位置可记为( )
| A. | (350,500) | B. | (-350,-500) | C. | (350,-500) | D. | (-350,500) |
 如图所示,将一个矩形ABCD纸片,剪去两个完全相同的矩形后,剩余的阴影部分纸片面积大小为24,且AB=8,则被剪掉的矩形的长为6.
如图所示,将一个矩形ABCD纸片,剪去两个完全相同的矩形后,剩余的阴影部分纸片面积大小为24,且AB=8,则被剪掉的矩形的长为6.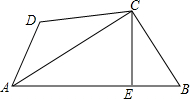 如图,已知四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且AE=$\frac{1}{2}$(AB+AD),若∠D=115°,则∠B=65°.
如图,已知四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且AE=$\frac{1}{2}$(AB+AD),若∠D=115°,则∠B=65°.