题目内容
17.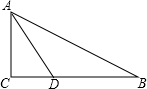 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,BD=5,求AC的长.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,BD=5,求AC的长.
分析 作DE⊥AB于E,根据角平分线的性质求出DE,根据勾股定理求出BE,根据勾股定理列出方程,解方程即可.
解答 解: 作DE⊥AB于E,
作DE⊥AB于E,
∵AD是∠BAC的平分线,∠C=90°,DE⊥AB,
∴DE=CD=3,AC=AE,
∴BE=$\sqrt{B{D}^{2}-D{E}^{2}}$=4,
设AC为x,则AB=x+4,
∴AC2+BC2=AB2,即x2+82=(x+4)2,
解得x=6,即AC的长为6.
点评 本题考查的是角平分线的性质和勾股定理的应用,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
7.下列事件中,属于随机事件的是( )
| A. | 掷一枚普通正六面体骰子,所得点数不超过6 | |
| B. | 买一张彩票中奖 | |
| C. | 太阳从西边落下 | |
| D. | 口袋中装有10个红球,从中摸出一个是白球 |
2.将点A(-3,3)向左平移3个单位长度,再向上平移5个单位长度则平移后点的坐标是( )
| A. | (0,8) | B. | (-6,-2) | C. | (0,-2) | D. | (-6,8) |
7.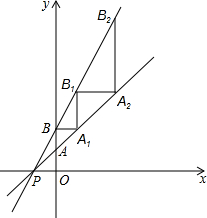 如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
 如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )| A. | (63,64) | B. | (65,64) | C. | (31,32) | D. | (127,128) |
 如图所示,将一个矩形ABCD纸片,剪去两个完全相同的矩形后,剩余的阴影部分纸片面积大小为24,且AB=8,则被剪掉的矩形的长为6.
如图所示,将一个矩形ABCD纸片,剪去两个完全相同的矩形后,剩余的阴影部分纸片面积大小为24,且AB=8,则被剪掉的矩形的长为6.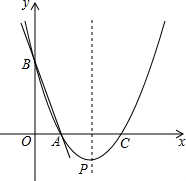 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.