题目内容
16.已知a、b是一元二次方程x2-x-2018=0的两个实数根,则代数式a2-2a-b的值等于2017.分析 先根据一元二次方程解的定义得到a2=a+2018,所以a2-2a-b化简为-(a+b)+2018,再利用根与系数的关系得到a+b=1,然后利用整体代入的方法计算.
解答 解:∵a为方程x2-x-2018=0的根,
∴a2-a-2018=0,
即a2=a+2018,
∴a2-2a-b=a+2018-2a-b=-(a+b)+2018,
∵a、b是一元二次方程x2-x-2018=0的两个实数根,
∴a+b=1,
所以原式=-1+2018=2017.
故答案为2017.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了一元二次方程解的定义.

练习册系列答案
相关题目
7.某校准备组织师生共80人,从温州乘坐动车前往雁落山参加夏令营活动,教师按成人票价购买,学生按学生票价购买,动车票价格如表所示:
若师生均购买二等座票,则共需1370元.
(1)参加活动的教师和学生各有多少人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.求y关于x的函数关系式.
| 运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
| 出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
| 温州南 | 雁落山 | 26 | 22 | 16 |
(1)参加活动的教师和学生各有多少人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.求y关于x的函数关系式.
5.若抛物线y=x2-4x+2-t(t为实数)在0<x<$\frac{5}{2}$的范围内与x轴有公共点,则t的取值范围为( )
| A. | -2<t<2 | B. | -2≤t<2 | C. | -$\frac{7}{4}$<t<2 | D. | t≥-2 |
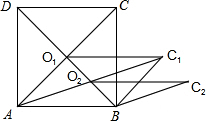 如图,正方形ABCD的面积为2$\sqrt{5}$cm2,对角线交于点O1,以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为$\frac{\sqrt{5}}{{2}^{5}}$cm2.
如图,正方形ABCD的面积为2$\sqrt{5}$cm2,对角线交于点O1,以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为$\frac{\sqrt{5}}{{2}^{5}}$cm2.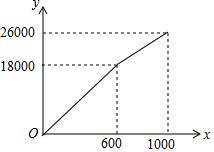 为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为${y}_{1}=\left\{\begin{array}{l}{{k}_{1}x(0≤x<600)}\\{{k}_{2}x+b(600≤x≤1000)}\end{array}\right.$,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.01x2-20x+30000(0≤x≤1000).
为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为${y}_{1}=\left\{\begin{array}{l}{{k}_{1}x(0≤x<600)}\\{{k}_{2}x+b(600≤x≤1000)}\end{array}\right.$,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.01x2-20x+30000(0≤x≤1000).