题目内容
5.若抛物线y=x2-4x+2-t(t为实数)在0<x<$\frac{5}{2}$的范围内与x轴有公共点,则t的取值范围为( )| A. | -2<t<2 | B. | -2≤t<2 | C. | -$\frac{7}{4}$<t<2 | D. | t≥-2 |
分析 先利用配方法得到抛物线的顶点为(2,-t),再分类讨论:当抛物线与x轴的公共点为顶点时,-t=0,解得t=0;当抛物线在0<x<3的范围内与x轴有公共点,如图,顶点在x轴下方,所以t>0,当抛物线在原点与对称轴之间与x轴有交点时,x=0,y>0,所以4-t>0,解得t<4;当抛物线在(3,0)与对称轴之间与x轴有交点时x=3,y>0,即1-t>0,解得t<1,所以此时t的范围为0<t<4,综上两种情况即可得到t的范围为0≤t<4.
解答 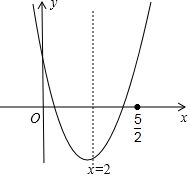 解:y=x2-4x+2-t=(x-2)2-2-t,
解:y=x2-4x+2-t=(x-2)2-2-t,
抛物线的顶点为(2,-2-t),
当抛物线与x轴的公共点为顶点时,-2-t=0,解得t=-2,
当抛物线在0<x<$\frac{5}{2}$的范围内与x轴有公共点,
如图,-t-2<0,解得t>-2,则x=0时,y>0,即2-t>0,解得t<2;
当x=$\frac{5}{2}$时,y>0,即-$\frac{7}{4}$-t>0,解得t<-$\frac{7}{4}$,此时t的范围为t<-$\frac{7}{4}$,
综上所述,t的范围为-2≤t<2.
故选B.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程.运用数形结合的思想是解决本题的关键.

练习册系列答案
相关题目
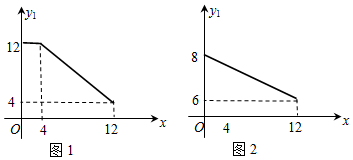
15.我市某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用80元;每日空置的客房,宾馆每日需支出40元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入-当日支出)
| x(元) | 180 | 210 | 260 | 300 |
| y(间) | 100 | 85 | 60 | 40 |
(2)已知每间入住的客房,宾馆每日需支出各种费用80元;每日空置的客房,宾馆每日需支出40元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入-当日支出)
13.下列算式正确的是( )
| A. | a2•a3=a6 | B. | x6÷x2=x3 | C. | (-2a3)2=-4a6 | D. | $\root{3}{-27}$=-3 |
14.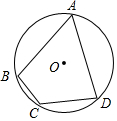 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |

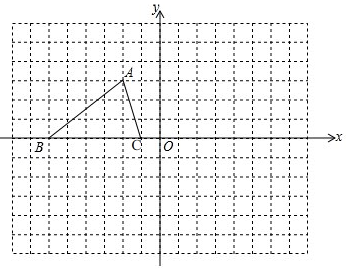 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).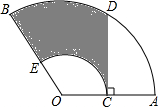 如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与$\widehat{AB}$交于点D,以O为圆心,OC的长为半径作$\widehat{CE}$交OB于点E,若OA=4,∠AOB=120°,则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$.(结果保留π)
如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与$\widehat{AB}$交于点D,以O为圆心,OC的长为半径作$\widehat{CE}$交OB于点E,若OA=4,∠AOB=120°,则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$.(结果保留π)