题目内容
20．已知$\frac{a-b}{a+b}=\frac{3}{7}$，则$\frac{a}{b}$=$\frac{5}{2}$．分析 根据比例的性质，可得二元一次方程，根据等式的性质，可得答案．
解答 解：由比例的性质，得
7a-7b=3a+3b，
由等式的性质，得
4a=10b．
$\frac{a}{b}$=$\frac{5}{2}$，
故答案为：$\frac{5}{2}$．
点评 本题考查了比例的性质，利用等式的性质是解题关键．
练习册系列答案
相关题目
2．
如图，已知四边形ABCD是平行四边形，要使它成为菱形，那么需要添加的条件可以是（ ）
如图，已知四边形ABCD是平行四边形，要使它成为菱形，那么需要添加的条件可以是（ ）| A． | AC⊥BD | B． | AB=AC | C． | ∠ABC=90° | D． | AC=BD |
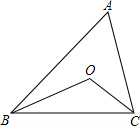如图，∠ABC=40°，∠ACB=60°，BO、CO平分∠ABC和∠ACB，则∠BOC=130°．
如图，△ADF≌△BCE，∠B=30°，∠F=25°，BC=5cm，CD=1cm，DF=4cm，则AC=4cm．
12．下列是二次根式的是（ ）
| A． | $\root{3}{2}$ | B． | $\sqrt{-2}$ | C． | $\sqrt{（-2）^{2}}$ | D． | $\sqrt{a}$ |
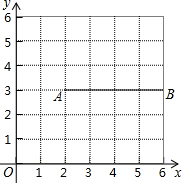如图所示，在平面直角坐标系中，已知点A（2，3）、B（6，3），连接AB．如果点P在直线y=x-1上，且点P到直线AB的距离小于1，那么称点P是线段AB的“邻近点”．若点P（m，n）是线段AB的“邻近点”，则m的取值范围是3＜m＜5．