题目内容
如图,已知二次函数图象的顶点为P(0,-1),且过点(2,3).点A是抛物线上一点,过点A作y轴的垂线,交抛物线于另一点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD.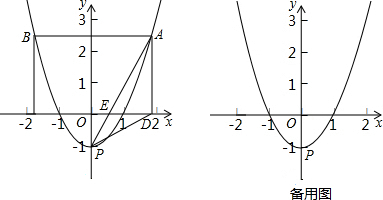
(1)求此二次函数的解析式;
(2)当点A在第一象限内时,PA与x轴交点记为E,证明:
①△PED∽△PDA;
②∠APC=90°;
(3)若∠APD=45°,当点A在y轴右侧时,请直接写出点A的坐标.
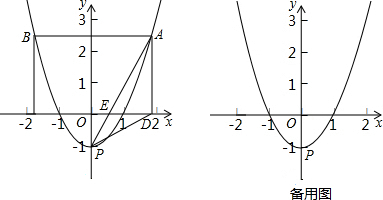
(1)求此二次函数的解析式;
(2)当点A在第一象限内时,PA与x轴交点记为E,证明:
①△PED∽△PDA;
②∠APC=90°;
(3)若∠APD=45°,当点A在y轴右侧时,请直接写出点A的坐标.
考点:二次函数综合题
专题:
分析:(1)直接利用待定系数法求求出a的值即可;
(2)①利用tan∠PDE=
,tan∠PAD=
=
,得出∠PDE=∠PAD,进而得出△PED∽△PDA;
②利用AC2=(2x)2+(x2-1)2=x4+2x2+1,PC2+PA2=12+x2+x2+(x2)2=x4+2x2+1
即可得出AC2=PC2+PA2,进而得出答案;
(3)利用H是过ACP三点的圆的圆心,D也在⊙H上,得出∠APC=90°,要满足∠APD=45°,则有∠AHD=90°,再利用等腰直角三角形的性质得出即可.
(2)①利用tan∠PDE=
| 1 |
| x |
| x |
| x2-1+1 |
| 1 |
| x |
②利用AC2=(2x)2+(x2-1)2=x4+2x2+1,PC2+PA2=12+x2+x2+(x2)2=x4+2x2+1
即可得出AC2=PC2+PA2,进而得出答案;
(3)利用H是过ACP三点的圆的圆心,D也在⊙H上,得出∠APC=90°,要满足∠APD=45°,则有∠AHD=90°,再利用等腰直角三角形的性质得出即可.
解答:解:(1)设抛物线解析式为y=ax2-1,将(2,3)点代入,
3=3a-1,
解得a=1,
∴抛物线解析式为y=x2-1;
(2)①如图,过P作AD垂线交AD延长线于点,
设A(x,x2-1),则tan∠PDE=
,tan∠PAD=
=
,
∴∠PDE=∠PAD,
又∵公共角∠EPD,
∴△PED∽△PDA,
②∵AC2=(2x)2+(x2-1)2=x4+2x2+1,
PC2+PA2=12+x2+x2+(x2)2=x4+2x2+1
∴AC2=PC2+PA2,
∴∠APC=90°;
(3)如备用图,∵点H为直角三角形ACP的斜边AC中点,
∴H是过ACP三点的圆的圆心,D也在⊙H上,
∵AC2=PC2+PA2,
∴∠APC=90°,要满足∠APD=45°,则有∠AHD=90°,
即2x=x2-1,
解得x=1±
,
∴A1(1+
,2+2
),A2(1-
,2-2
),
(方法不唯一,也可用代数方法解决).
3=3a-1,
解得a=1,
∴抛物线解析式为y=x2-1;
(2)①如图,过P作AD垂线交AD延长线于点,
设A(x,x2-1),则tan∠PDE=
| 1 |
| x |
| x |
| x2-1+1 |
| 1 |
| x |
∴∠PDE=∠PAD,
又∵公共角∠EPD,
∴△PED∽△PDA,
②∵AC2=(2x)2+(x2-1)2=x4+2x2+1,
PC2+PA2=12+x2+x2+(x2)2=x4+2x2+1
∴AC2=PC2+PA2,

∴∠APC=90°;
(3)如备用图,∵点H为直角三角形ACP的斜边AC中点,
∴H是过ACP三点的圆的圆心,D也在⊙H上,
∵AC2=PC2+PA2,
∴∠APC=90°,要满足∠APD=45°,则有∠AHD=90°,
即2x=x2-1,
解得x=1±
| 2 |
∴A1(1+
| 2 |
| 2 |
| 2 |
| 2 |
(方法不唯一,也可用代数方法解决).
点评:此题主要考查了二次函数的综合应用以及相似三角形的判定与性质和锐角三角函数关系等知识,熟练利用勾股定理逆定理得出直角三角形是解题关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
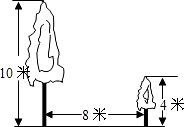 如图,有两棵树,一棵高10米,另一棵树高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
如图,有两棵树,一棵高10米,另一棵树高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )| A、8米 | B、10米 |
| C、12米 | D、14米 |
3的绝对值是( )
| A、-3 | ||
| B、3 | ||
C、
| ||
D、-
|
 如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上;
已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上;