题目内容
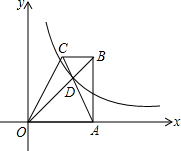 已知直角梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,对角线AC、BO相交于点D,双曲线y=
已知直角梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,对角线AC、BO相交于点D,双曲线y=| k |
| x |
考点:直角梯形,反比例函数系数k的几何意义
专题:
分析:根据△BCD∽△OAD,利用相似三角形的面积的比等于相似比的平方即可求得△OAD的面积,作DE⊥OA于点E,则DE∥AB,据此即可求得OE与OA的比值,根据三角形的面积公式即可求得△ODE的面积,根据反比例函数比例系数k的几何意义即可求解.
解答: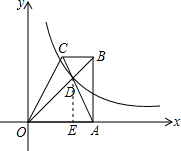 解:作DE⊥OA于点E.
解:作DE⊥OA于点E.
∵BC∥AO,
∴△BCD∽△OAD,
∴
=(
)2=
,
=
=2,
∴S△OAD=12,
∵BC∥AO,
∴
=
=2,
∴OE=
OA,
∴S△OAD=
S△OAD=
×12=8,
∴k=16.
故答案是:16.
 解:作DE⊥OA于点E.
解:作DE⊥OA于点E.∵BC∥AO,
∴△BCD∽△OAD,
∴
| S△BCD |
| S△OAD |
| BC |
| OA |
| 1 |
| 4 |
| OD |
| BD |
| OA |
| BC |
∴S△OAD=12,
∵BC∥AO,
∴
| OE |
| AE |
| OD |
| BD |
∴OE=
| 2 |
| 3 |
∴S△OAD=
| 2 |
| 3 |
| 2 |
| 3 |
∴k=16.
故答案是:16.
点评:本题考查了相似三角形的性质以及反比例函数的几何意义,根据相似三角形的性质以及三角形的面积公式求得△ODE的面积是关键.

练习册系列答案
相关题目
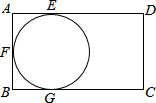 如图,⊙O分别切矩形ABCD的边于E、F、G三点,点P在⊙O上,且不与E、F、G重合,则∠EPF等于( )
如图,⊙O分别切矩形ABCD的边于E、F、G三点,点P在⊙O上,且不与E、F、G重合,则∠EPF等于( )| A、45° |
| B、90° |
| C、45°或135° |
| D、45°或90° |
 已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上;
已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上;