题目内容
8.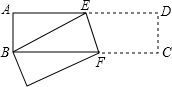 已知,如图长方形ABCD中,AB=6cm,AD=18cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为8cm.
已知,如图长方形ABCD中,AB=6cm,AD=18cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为8cm.
分析 根据折叠的性质可得BE=DE,从而设AE即可表示BE,在直角三角形AEB中,根据勾股定理列方程即可求解.
解答 解:设AE=xcm,则BE=DE=(18-x)cm,
在Rt△ABE中,BE2=AE2+AB2,即(18-x)2=x2+62,
解得:x=8.
故答案为8cm.
点评 此题考查了翻折变换的知识,解答本题的关键是掌握翻折前后对应线段相等,另外要熟练运用勾股定理解直角三角形.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
18.如果a表示一个负数,则|a|等于( )
| A. | a | B. | 0 | C. | -a | D. | 不确定 |
3.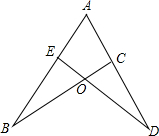 如图,若已知AE=AC,用“SAS”说明△ABC≌△ADE,还需要的一个条件是( )
如图,若已知AE=AC,用“SAS”说明△ABC≌△ADE,还需要的一个条件是( )
 如图,若已知AE=AC,用“SAS”说明△ABC≌△ADE,还需要的一个条件是( )
如图,若已知AE=AC,用“SAS”说明△ABC≌△ADE,还需要的一个条件是( )| A. | BC=DE | B. | AB=AD | C. | BO=DO | D. | EO=CO |
20.甲乙两种水稻试验品中连续5年的平均单位面积产量如下(单位:吨/公顷)
(1)甲乙两种水稻试验品的中位数分别是多少?
(2)甲乙两种水稻试验品的平均数分别是多少?
(3)试根据这组数据估计哪中水稻品种的产量比较稳定.
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
(2)甲乙两种水稻试验品的平均数分别是多少?
(3)试根据这组数据估计哪中水稻品种的产量比较稳定.
17. 如图,△ABC中,MN∥BC,MC与BN相交于点O,如果AM:MB=1:2,则NO:OB=( )
如图,△ABC中,MN∥BC,MC与BN相交于点O,如果AM:MB=1:2,则NO:OB=( )
 如图,△ABC中,MN∥BC,MC与BN相交于点O,如果AM:MB=1:2,则NO:OB=( )
如图,△ABC中,MN∥BC,MC与BN相交于点O,如果AM:MB=1:2,则NO:OB=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
18. 如图,DE∥GF,A在DE上,C在GF上△ABC为等边三角形,其中∠EAC=80°,则∠BCG度数为( )
如图,DE∥GF,A在DE上,C在GF上△ABC为等边三角形,其中∠EAC=80°,则∠BCG度数为( )
 如图,DE∥GF,A在DE上,C在GF上△ABC为等边三角形,其中∠EAC=80°,则∠BCG度数为( )
如图,DE∥GF,A在DE上,C在GF上△ABC为等边三角形,其中∠EAC=80°,则∠BCG度数为( )| A. | 10° | B. | 20° | C. | 25° | D. | 30° |
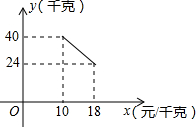 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题: