题目内容
13. 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:(1)甲先出发3小时后,乙才出发;大约在甲出发4小时后,两人相遇,这时他们离A地40千米;
(2)两人的行驶速度分别是多少?
(3)分别写出表示甲、乙的路程y(千米)与时间x(小时)之间的函数表达式(不要求写出自变量的取值范围).
分析 (1)结合图象,依据点的坐标代表的意思,即可得出结论;
(2)由速度=路程÷时间,即可得出结论;
(3)根据待定系数法,可求出乙的函数表达式,结合甲的速度依据甲的图象过原点,可得出甲的函数表达式.
解答 解:(1)结合图象可知,甲出发3小时后,乙才出发;大约在甲出发4个小时后,两人相遇,这时他们离A地40千米.
故答案为:3;4;40.
(2)甲的速度:80÷8=10km/h;
乙的速度:80÷(5-3)=40km/h.
(3)∵甲的速度为10km/h,且过原点(0,0),
∴甲的函数表达式:y=10x;
设乙的函数表达式为y=kx+b,
∵点(3,0)和(5,80)在乙的图象上,
∴有$\left\{\begin{array}{l}{0=3k+b}\\{80=5k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=40}\\{b=-120}\end{array}\right.$.
故乙的函数表达式:y=40x-120.
点评 本题考查了一次函数中的相遇问题、用待定系数法求函数表达式,解题的关键是:(1)明白坐标系里点的坐标代表的意义;(2)知道速度=路程÷时间;(3)会用待定系数法求函数表达式.本题难度不大,属于基础题,做此类问题是,结合函数图象,找出点的坐标才能做对题.

练习册系列答案
相关题目
4.二次函数y=-(x+1)2-4的图象的顶点坐标是( )
| A. | (1,-4) | B. | (-1,4) | C. | (-1,-4) | D. | (1,4) |
1.点(4,-5)关于y轴的对称点的坐标是( )
| A. | (4,5) | B. | (-4,-5) | C. | (-4,5) | D. | (-5,4) |
5.已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a+b的值是( )
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
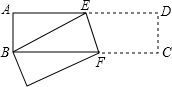 已知,如图长方形ABCD中,AB=6cm,AD=18cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为8cm.
已知,如图长方形ABCD中,AB=6cm,AD=18cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为8cm.