题目内容
16.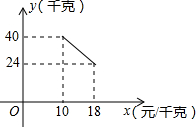 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式;若你是商场负责人,会将销售价定为多少,来保证每天的销售利润最大?最大利润是多少?
分析 (1)由图象可知y与x之间是一次函数关系,可设y=kx+b,把(10,40),(18,24)代入可得;
(2)根据:销售利润W=该产品每千克利润×销售量,列出函数关系式,配成二次函数顶点式,结合自变量取值范围可得其最值.
解答 解:(1)设y与x之间的函数关系式:y=kx+b,
把(10,40),(18,24)代入得:
$\left\{\begin{array}{l}{10k+b=40}\\{18k+b=24}\end{array}\right.$,
解得:$\left\{\begin{array}{l}k=-2\\ b=60\end{array}\right.$,
∴y与x之间的函数关系式y=-2x+60(10≤x≤18);
(2)W=(x-10)(-2x+60)
=-2x2+80x-600
=-2(x-20)2+200,
∴当x<20时,w随着x的增大而增大,
∵10≤x≤18,
∴当x=18时,W最大,最大为192.
即当销售价为18元时,每天的销售利润最大,最大利润是192元.
点评 本题主要考查二次函数的应用能力,结合函数图象待定系数法求函数解析式是基本能力,确定利润最大值通常利用二次函数来解决,根据题意找到相等关系列出函数解析式是解题关键.

练习册系列答案
相关题目
4.二次函数y=-(x+1)2-4的图象的顶点坐标是( )
| A. | (1,-4) | B. | (-1,4) | C. | (-1,-4) | D. | (1,4) |
11.正五边形的中心角等于( )
| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
1.点(4,-5)关于y轴的对称点的坐标是( )
| A. | (4,5) | B. | (-4,-5) | C. | (-4,5) | D. | (-5,4) |
5.已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a+b的值是( )
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
6.下列四个几何体中,左视图与其它三个不同的是( )
| A. |  | B. |  | C. |  | D. |  |
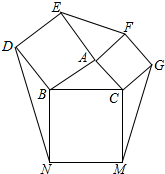 如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN
如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN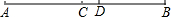 如图,C是线段AB的中点,D在线段CB上,AD=6,DB=4,则CD的长等于1.
如图,C是线段AB的中点,D在线段CB上,AD=6,DB=4,则CD的长等于1.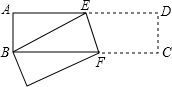 已知,如图长方形ABCD中,AB=6cm,AD=18cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为8cm.
已知,如图长方形ABCD中,AB=6cm,AD=18cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为8cm.