题目内容
17. 如图,△ABC中,MN∥BC,MC与BN相交于点O,如果AM:MB=1:2,则NO:OB=( )
如图,△ABC中,MN∥BC,MC与BN相交于点O,如果AM:MB=1:2,则NO:OB=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
分析 根据AM:MB的比值可求出MN:BC的比值,由MN∥BC易证△MNO∽△CBO,再由相似三角形的性质:对应边的比值相等即可求出NO:OB的值.
解答 解:∵MN∥BC,AM:MB=1:2,
∴AM:AB=MN:BC=1:3,
∵MN∥BC,
∴△MNO∽△CBO,
∴NO:BO=MN:BC=1:3,
故选B.
点评 本题考查了相似三角形的判定和性质,求出MN:BC的值是解题关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
5.已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a+b的值是( )
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
12.下列计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | 18$\frac{1}{2}$-5$\frac{1}{2}$=13$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{2}{3}$ | D. | -32=-9 |
9.下列计算正确的是( )
| A. | ($\frac{1}{3}$)-2=9 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | (-3)0=-1 | D. | |-7-5|=2 |
6.下列四个几何体中,左视图与其它三个不同的是( )
| A. |  | B. |  | C. |  | D. |  |
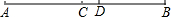 如图,C是线段AB的中点,D在线段CB上,AD=6,DB=4,则CD的长等于1.
如图,C是线段AB的中点,D在线段CB上,AD=6,DB=4,则CD的长等于1.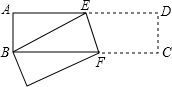 已知,如图长方形ABCD中,AB=6cm,AD=18cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为8cm.
已知,如图长方形ABCD中,AB=6cm,AD=18cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为8cm.