题目内容
20.甲乙两种水稻试验品中连续5年的平均单位面积产量如下(单位:吨/公顷)| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
(2)甲乙两种水稻试验品的平均数分别是多少?
(3)试根据这组数据估计哪中水稻品种的产量比较稳定.
分析 (1)根据中位数的定义解答即可;
(2)根据平均数的定义解答即可;
(3)根据方差进行解答即可.
解答 解:(1)甲乙两种水稻试验品的中位数分别是10.05,10.05;
(2)甲乙两种水稻试验品的平均数分别是10,10;
(3)甲水稻品种的方差为:$\frac{1}{5}$×[(9.8-10)2+(9.9-10)2+(10.1-10)2+(10-10)2+(10.2-10)2]=0.02;
乙水稻品种的方差为:$\frac{1}{5}$×[(9.4-10)2+(10.3-10)2+(10.8-10)2+(9.7-10)2+(9.8-10)2]=0.124,
所以甲水稻品种的产量比较稳定.
点评 本题考查了平均数、方差问题,关键是根据给出两组数据,要求我们比较它们的平均数与方差的大小.

练习册系列答案
相关题目
11.正五边形的中心角等于( )
| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
15.估计$\sqrt{7}$+2的值在( )
| A. | 2到3之间 | B. | 3到4之间 | C. | 4到5之间 | D. | 5到6之间 |
5.已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a+b的值是( )
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
12.下列计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | 18$\frac{1}{2}$-5$\frac{1}{2}$=13$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{2}{3}$ | D. | -32=-9 |
9.下列计算正确的是( )
| A. | ($\frac{1}{3}$)-2=9 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | (-3)0=-1 | D. | |-7-5|=2 |
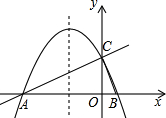 如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A,C两点,与x轴的另一交点为点B.
如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A,C两点,与x轴的另一交点为点B.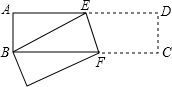 已知,如图长方形ABCD中,AB=6cm,AD=18cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为8cm.
已知,如图长方形ABCD中,AB=6cm,AD=18cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为8cm.