题目内容
8. 如图,在平面直角坐标系xOy中,点A(0,m+4),点C(5m+3,0)在x轴的正半轴上,现将点C向左平移4单位长度再向上平移7个单位长度得到对应点B(7m-7,n).
如图,在平面直角坐标系xOy中,点A(0,m+4),点C(5m+3,0)在x轴的正半轴上,现将点C向左平移4单位长度再向上平移7个单位长度得到对应点B(7m-7,n).(1)求m,n的值;
(2)若点P从点C出发以每秒2个单位长度/秒的速度沿CO方向移动,同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动,设移动的时间为t秒(0<t<7),四边形OPBA与△OQB的面积分别记为S1,S2.是否存在一段时间,使S1<2S2?若存在,求出t的取值范围;若不存在,试说明理由.
分析 (1)根据点C向左平移4单位长度再向上平移7个单位长度得到对应点B,列方程组解出即可;
(2)先根据动点P、Q的速度表示出路程分别为:2t、t,再根据面积公式表示出S1和S2,代入S1<2S2列不等式求t的取值范围,并与0<t<7相结合得出t的取值.
解答 解:(1)由题意得:$\left\{\begin{array}{l}{n=7}\\{5m+3-(7m-7)=4}\end{array}\right.$
解得:m=3,n=7,
(2)存在,如图,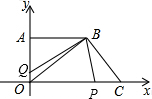
由(1)得:A(0,7),B(14,7),C(18,0),
由题意得:PC=2t,OQ=t,则OP=18-2t,
S1=$\frac{1}{2}$(AB+OP)×OA=$\frac{1}{2}$×(14+18-2t)×7=-7t+112,
${S_2}=\frac{1}{2}t×14$=7t,
∵要满足S1<2S2,
∴-7t+112<2×7t,
t>$\frac{16}{3}$,
又∵0<t<7,
∴当$\frac{16}{3}$<t<7时,S1<2S2.
点评 本题是几何变换的综合题,考查了点的坐标与平移的关系,还考查了动点在运动过程中所形成的图形面积问题,此类题的解题思路为:先表示动点的路程,再根据图形形状直接或间接利用和、差表示图形面积.

练习册系列答案
相关题目
19. 如图,三角形ABC沿BC边所在的直线向左平移得到三角形DEF,下列说法错误的是( )
如图,三角形ABC沿BC边所在的直线向左平移得到三角形DEF,下列说法错误的是( )
 如图,三角形ABC沿BC边所在的直线向左平移得到三角形DEF,下列说法错误的是( )
如图,三角形ABC沿BC边所在的直线向左平移得到三角形DEF,下列说法错误的是( )| A. | DE∥AB | B. | ∠D=∠A | C. | AC=DF | D. | ∠D=∠DEF |
17.下列算式正确的( )
| A. | $\frac{(-a+b)^{2}}{(a-b)^{2}}$=1 | B. | $\frac{-a-1}{-a^2+8}$=$\frac{a-1}{a^2+8}$ | ||
| C. | $\frac{x^2+y^2}{x+y}$=x+y | D. | $\frac{0.5+2y}{0.1+x}$=$\frac{5+2y}{1+x}$ |
18. 在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDC的面积为( )
在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDC的面积为( )
 在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDC的面积为( )
在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDC的面积为( )| A. | 2$\sqrt{2}$-2 | B. | 3$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |




 过平行四边形纸片的一个顶点作一条线段,沿这条线段剪下一个三角形纸片,将它平移到右边的位置,可得到新的平行四边形.
过平行四边形纸片的一个顶点作一条线段,沿这条线段剪下一个三角形纸片,将它平移到右边的位置,可得到新的平行四边形.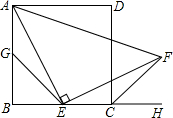 如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.
如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG. 如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相较于点M,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.
如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相较于点M,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.