题目内容
15.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.(1)c=30,b=20;
(2)∠B=72°,c=14;
(3)∠B=30°,a=$\sqrt{7}$.
分析 (1)利用勾股定理列式求出c,再根据∠B的正值求出∠B,然后根据直角三角形两锐角互余求出∠A;
(2)根据直角三角形两锐角互余求出∠A,利用∠A,∠B的正弦列式求出a,b;
(3)根据直角三角形两锐角互余求出∠A,利用∠A,的正弦列式求出c,根据勾股定理求得b.
解答 解:(1)由勾股定理得,a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{3{0}^{2}-2{0}^{2}}$=10$\sqrt{5}$,
∵sinB=$\frac{b}{c}$=$\frac{2}{3}$,
∴∠B≈42°,
∴∠A=90°-42°=48°,
(2)∵∠B=72°,
∴∠A=90°-∠B=18°,
∵sinA=$\frac{a}{c}$=0.309,sinB=$\frac{b}{c}$=0.951,
∴a=4.326,b=13.31;
(3)∵∠B=30°,
∴∠A=60°,
∴sinA=$\frac{a}{c}$=$\frac{\sqrt{3}}{2}$,
∴c=$\frac{2\sqrt{21}}{3}$,
由勾股定理得b=$\sqrt{{c}^{2}-{a}^{2}}$=$\frac{\sqrt{21}}{3}$.
点评 本题考查了解直角三角形,主要利用了锐角三角函数和勾股定理解决问题.

练习册系列答案
相关题目
6. 如图,数轴上点A所表示的数的相反数的倒数是( )
如图,数轴上点A所表示的数的相反数的倒数是( )
 如图,数轴上点A所表示的数的相反数的倒数是( )
如图,数轴上点A所表示的数的相反数的倒数是( )| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
5.截止年底,某市人口总数已达到4230000人,将4230000用科学记数法表示为( )
| A. | 0.423×107 | B. | 4.23×106 | C. | 42.3×105 | D. | 423×104 |
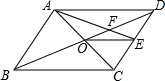 如图,点O是?ABCD的对角线交点,E为CD中点,AE交BD于点F,若S△AOE=3,则S△AOB的值为6.
如图,点O是?ABCD的对角线交点,E为CD中点,AE交BD于点F,若S△AOE=3,则S△AOB的值为6. 如图,△BDC与△CEB在线段BC的同侧,CD与BE相交于点A,∠ABC=∠ACB,AD=AE,求证:BD=CE.
如图,△BDC与△CEB在线段BC的同侧,CD与BE相交于点A,∠ABC=∠ACB,AD=AE,求证:BD=CE. 在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.