题目内容
3.先化简,再求值:($\frac{1}{x-1}$-$\frac{1}{x+1}$)÷$\frac{x+2}{{{x^2}-1}}$,其中x=2sin30°+2$\sqrt{2}$cos45°.分析 根据分式的混合运算顺序和法则先化简原式,再根据特殊锐角的三角函数值求得x的值,代入计算可得.
解答 解:原式=$\frac{(x+1)-(x-1)}{{{x^2}-1}}$÷$\frac{x+2}{{{x^2}-1}}$
=$\frac{2}{{{x^2}-1}}$×$\frac{{{x^2}-1}}{x+2}$
=$\frac{2}{x+2}$
∵x=2sin30°+2$\sqrt{2}$cos45°
=2×$\frac{1}{2}$+2$\sqrt{2}$×$\frac{{\sqrt{2}}}{2}$=3,
∴原式=$\frac{2}{3+2}=\frac{2}{5}$.
点评 本题主要考查分式的化简求值及特殊锐角的三角函数值,熟练掌握分式的混合运算顺序和法则是解题的关键.

练习册系列答案
相关题目
13.下列式子中是分式的是( )
| A. | $\frac{10x}{7}$ | B. | $\frac{9+x}{5}$ | C. | $\frac{100}{20+x}$ | D. | $\frac{2}{5}$ |
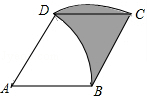 菱形ABCD的边长为2$\sqrt{3}$m,∠A=60°,弧CD是以点B为圆心,BC长为半径的弧,弧BD是以A为圆心,AB长为半径的弧,则阴影部分面积为3$\sqrt{3}$m2.(结果保留根号)
菱形ABCD的边长为2$\sqrt{3}$m,∠A=60°,弧CD是以点B为圆心,BC长为半径的弧,弧BD是以A为圆心,AB长为半径的弧,则阴影部分面积为3$\sqrt{3}$m2.(结果保留根号) 如图,在平面直角坐标系中,直线l:y=x-1与x轴交于点A,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1,…,正方形AnBnCnCn-1,使得点A1、A2、A3…An在直线l上,点C1、C2、C3…Cn在y轴正半轴上,请解决下列问题:
如图,在平面直角坐标系中,直线l:y=x-1与x轴交于点A,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1,…,正方形AnBnCnCn-1,使得点A1、A2、A3…An在直线l上,点C1、C2、C3…Cn在y轴正半轴上,请解决下列问题: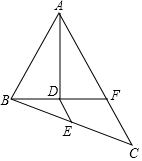 如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于 点F,E为BC的中点,求DE的长.
如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于 点F,E为BC的中点,求DE的长.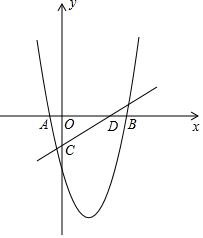 如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=$\frac{3}{4}$x-3与y轴交于点C,与x轴交于点D,点P时第四象限内的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.
如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=$\frac{3}{4}$x-3与y轴交于点C,与x轴交于点D,点P时第四象限内的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.