题目内容
18.(1)计算:($\frac{1}{2}$)-1+|1-$\sqrt{3}$|-(π-3)0-$\root{3}{8}$;(2)化简:$\frac{a-1}{a+2}$•$\frac{{a}^{2}-4}{{a}^{2}-2a+1}$÷$\frac{1}{1-{a}^{2}}$;
(3)解不等式组:$\left\{\begin{array}{l}{5x+2≥3x-6}\\{\frac{x-2}{6}>\frac{x}{2}-1}\end{array}\right.$,并写出它的非负整数解.
(4)关于x的一元二次方程x2-(2m-1)x+m2+1=0.设x1,x2分别是方程的两个根,且满足x12+x22=x1x2+10,求实数m的值.
分析 (1)将($\frac{1}{2}$)-1=2、(π-3)0=1、$\root{3}{8}$=$\sqrt{2}$代入原式,再根据实数的运算即可得出结论;
(2)根据完全平方差、完全平凡公式结合分式的运算,即可得出结论;
(3)根据不等式组的解法及步骤,解不等式组即可得出x的取值范围,取其内的非负整数即可;
(4)根据方程有两个实数根结合根的判别式即可得出△=-4m-3≥0,解之即可得出m的取值范围,再根据根与系数的关系结合x12+x22=x1x2+10即可得出关于m的一元二次方程,解之即可得出结论.
解答 解:(1)($\frac{1}{2}$)-1+|1-$\sqrt{3}$|-(π-3)0-$\root{3}{8}$,
=2+$\sqrt{3}$-1-1-$\sqrt{2}$,
=$\sqrt{3}$-$\sqrt{2}$.
(2)原式=$\frac{a-1}{a+2}$•$\frac{(a+2)(a-2)}{(a-1)^{2}}$÷$\frac{1}{(1+a)(1-a)}$,
=$\frac{a-1}{a+2}$•$\frac{(a+2)(a-2)}{(a-1)^{2}}$•(1+a)(1-a),
=-(a-2)(1+a),
=-a2+a+2.
(3)$\left\{\begin{array}{l}{5x+2≥3x-6①}\\{\frac{x-2}{6}>\frac{x}{2}-1②}\end{array}\right.$,
解不等式①,得:x≥-4;
解不等式②,得:x<2.
∴不等式组的解为-4≤x<2.
∴x=0和1.
(4)∵方程x2-(2m-1)x+m2+1=0有两个实数根,
∴△=[-(2m-1)]2-4(m2+1)=-4m-3≥0,
∴m≤-$\frac{3}{4}$.
∵x1,x2是方程x2-(2m-1)x+m2+1=0的两个根,
∴x1+x2=2m-1,x1•x2=m2+1,
∴x12+x22=$({x}_{1}+{x}_{2})^{2}$-2x1x2=x1x2+10,即(2m-1)2-2(m2+1)=m2+1+10,
解得:m=-2或m=6(舍去).
∴实数m的值为-2.
点评 本题考查了根与系数的关系、根的判别式、实数的运算、零指数幂、负整数指数幂、解一元一次不等式组、一元一次不等式组的整数解以及解一元二次方程,解题的关键是:(1)熟练掌握实数的运算顺序;(2)利用消元法将原式进行化简;(3)熟练掌握解一元一次不等式的方法及步骤;(4)根据根与系数的关系以及根的判别式找出关于m的一元一次不等式以及一元二次方程.

 如图,在平面直角坐标系中,四边形ABCD是梯形,AD∥BC,E是BC的中点,BC=12,点A坐标是(0,4),CD所在直线的函数关系式为y=-x+9,点P是BC边上一个动点,
如图,在平面直角坐标系中,四边形ABCD是梯形,AD∥BC,E是BC的中点,BC=12,点A坐标是(0,4),CD所在直线的函数关系式为y=-x+9,点P是BC边上一个动点,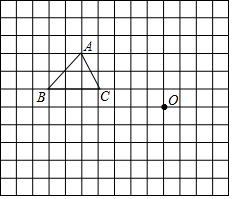 如图,△ABC是格点三角形,按下列要求作图:
如图,△ABC是格点三角形,按下列要求作图: