题目内容
13.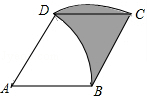 菱形ABCD的边长为2$\sqrt{3}$m,∠A=60°,弧CD是以点B为圆心,BC长为半径的弧,弧BD是以A为圆心,AB长为半径的弧,则阴影部分面积为3$\sqrt{3}$m2.(结果保留根号)
菱形ABCD的边长为2$\sqrt{3}$m,∠A=60°,弧CD是以点B为圆心,BC长为半径的弧,弧BD是以A为圆心,AB长为半径的弧,则阴影部分面积为3$\sqrt{3}$m2.(结果保留根号)
分析 连接BD,过点D作DE⊥BC,垂足为E,由四边形ABCD是菱形,∠A=60°可知△ABD及△BCD是等边三角形,故阴影部分的面积等于△BCD的面积,再求出DE的长,由三角形的面积公式即可得出结论.
解答 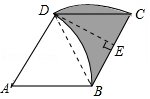 解:连接BD,过点D作DE⊥BC,垂足为E,
解:连接BD,过点D作DE⊥BC,垂足为E,
∵四边形ABCD是菱形,∠A=60°,
∴△ABD及△BCD是等边三角形,
∴S阴影=S△BCD=$\frac{1}{2}$BC•DE=$\frac{1}{2}$×2$\sqrt{3}$×2$\sqrt{3}$×sin60°=3$\sqrt{3}$m2.
故答案为:3$\sqrt{3}$.
点评 本题考查的是扇形面积的计算及菱形的性质,根据题意作出辅助线,得出S阴影=S△BCD是解答此题的关键.

练习册系列答案
相关题目
1.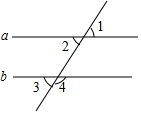 如图,根据下列条件不可以判定a∥b的是( )
如图,根据下列条件不可以判定a∥b的是( )
 如图,根据下列条件不可以判定a∥b的是( )
如图,根据下列条件不可以判定a∥b的是( )| A. | ∠2=∠3 | B. | ∠1=∠3 | C. | ∠1=∠4 | D. | ∠1+∠4=180° |
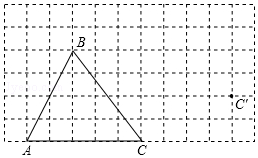 画图并填空:
画图并填空: