题目内容
19.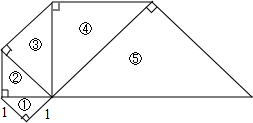 一系列等腰直角三角形组成的螺旋形如图所示,其序号依次为①,②,③,④,⑤,…,则第n等腰直角三角形的斜边长为($\sqrt{2}$)n.
一系列等腰直角三角形组成的螺旋形如图所示,其序号依次为①,②,③,④,⑤,…,则第n等腰直角三角形的斜边长为($\sqrt{2}$)n.
分析 根据图形,先求出第一个等腰直角三角形的斜边,再在此基础上求出第二个等腰直角三角形是斜边,…以此类推,从而可求出第n个等腰直角三角形的斜边.
解答 解:如右图所示,
第一个等腰直角三角形的斜边=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
第二个等腰直角三角形的斜边=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=($\sqrt{2}$)2=2,
第三个等腰直角三角形的斜边=$\sqrt{{2}^{2}+{2}^{2}}$=($\sqrt{2}$)3,
…,
第n个等腰直角三角形的斜边=($\sqrt{2}$)n,
故答案是:($\sqrt{2}$)n.
点评 本题考查了等腰三角形的性质,勾股定理.关键是利用勾股定理求出每一个等腰直角三角形的斜边.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
9. 如图,PQ∥BC,若S△APQ=3,S△PQB=6,则S△CQB等于( )
如图,PQ∥BC,若S△APQ=3,S△PQB=6,则S△CQB等于( )
 如图,PQ∥BC,若S△APQ=3,S△PQB=6,则S△CQB等于( )
如图,PQ∥BC,若S△APQ=3,S△PQB=6,则S△CQB等于( )| A. | 20 | B. | 18 | C. | 16 | D. | 9 |
7.若一元二次方程x2-ax-4a=0的两实根之和为4a2-3,则两实根之积为( )
| A. | -4 | B. | 3或-4 | C. | 3 | D. | -3或4 |
 如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.
如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.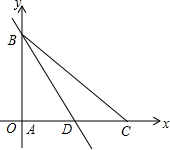 如图,△ABC中,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC、AB所在直线为x轴、y轴建立直角坐标系.
如图,△ABC中,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC、AB所在直线为x轴、y轴建立直角坐标系.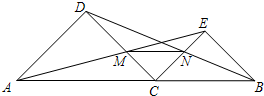 如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N.
如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N.