题目内容
4.解下列分式方程:(1)$\frac{2-x}{x-3}$+$\frac{1}{3-x}$=1
(2)$\frac{2x}{x+1}$=1-$\frac{x}{3x+3}$.
分析 (1)分式方程变形后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:2-x-1=x-3,
解得:x=3,
经检验x=3是分式方程的解;
(2)去分母得:6x=3x+3-x,
解得:x=$\frac{3}{4}$,
经检验x=$\frac{3}{4}$是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
15.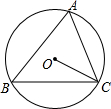 如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )
如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )
 如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )
如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )| A. | 15° | B. | 18° | C. | 20° | D. | 28° |
12.下列说法正确的是( )
| A. | 角的边越长,角度就越大 | B. | 周角就是一条射线 | ||
| C. | 一条直线可以看成平角 | D. | 平角的两边可以构成一条直线 |
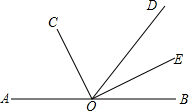 如图所示,已知点A、O、B在同一条直线上,且OC、OE分别是∠AOD、∠BOD的角平分线,若∠BOD=72°,求∠COD和∠COE的度数.
如图所示,已知点A、O、B在同一条直线上,且OC、OE分别是∠AOD、∠BOD的角平分线,若∠BOD=72°,求∠COD和∠COE的度数.