题目内容
19.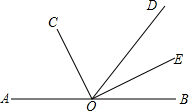 如图所示,已知点A、O、B在同一条直线上,且OC、OE分别是∠AOD、∠BOD的角平分线,若∠BOD=72°,求∠COD和∠COE的度数.
如图所示,已知点A、O、B在同一条直线上,且OC、OE分别是∠AOD、∠BOD的角平分线,若∠BOD=72°,求∠COD和∠COE的度数.
分析 根据角平分线定义和已知得出∠BOE=∠DOE=$\frac{1}{2}$∠BOD=36°,∠AOC=∠COD=$\frac{1}{2}$∠AOD,∠AOD=180°-∠BOD=108°,求出∠DOC即可.
解答 解:∵OC、OE分别是∠AOD、∠BOD的角平分线,∠BOD=72°,
∴∠BOE=∠DOE=$\frac{1}{2}$∠BOD=36°,∠AOC=∠COD=$\frac{1}{2}$∠AOD,∠AOD=180°-∠BOD=108°,
∴∠DOC=∠AOC=$\frac{1}{2}$×108°=54°,
∴∠COE=∠COD+∠DOE=54°+36°=90°.
点评 本题考查了角平分线定义的应用,解此题的关键是能根据角平分线定义得出∠BOE=∠DOE=$\frac{1}{2}$∠BOD,∠AOC=∠COD=$\frac{1}{2}$∠AOD,难度不是很大.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
10.菱形具有而一般平行四边形不具有的性质是( )
| A. | 对边相等 | B. | 对角相等 | C. | 对角线互相垂直 | D. | 对角线互相平分 |
14.计算(-ax-1)4结果是( )
| A. | a4x-1 | B. | -a4x-4 | C. | a4x-4 | D. | -a4x-1 |
11.为了迎接“五•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价-进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?该专卖店要获得最大利润应如何进货?
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 240 | 160 |
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价-进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?该专卖店要获得最大利润应如何进货?
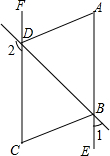 如图,已知∠1+∠2=180°,∠A=∠C,试说明AD∥BC的理由.
如图,已知∠1+∠2=180°,∠A=∠C,试说明AD∥BC的理由.