Question

13．连接对角线相等的四边形，它的中点四边形是：菱形，菱形的中点四边形是：矩形．

Answer 1

分析 因为四边形的两条对角线相等，根据三角形的中位线定理，可得所得的四边形的四边相等，则所得的四边形是菱形；根据三角形的中位线定理以及菱形的性质即可．

解答 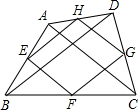解：如图，AC=BD，E、F、G、H分别是线段AB、BC、CD、AD的中点，
则EH、FG分别是△ABD、△BCD的中位线，EF、HG分别是△ACD、△ABC的中位线，
根据三角形的中位线的性质知，EH=FG=$\frac{1}{2}$BD，EF=HG=$\frac{1}{2}$AC，
∵AC=BD，
∴EH=FG=FG=EF，
∴四边形EFGH是菱形；
当四边形ABCD是菱形时，AC⊥BD，
∵EH∥BD，
∴AC⊥EH，
∵EF∥AC，
∴EF⊥EH，
∴平行四边形EFGH是矩形．
故答案为：菱形；矩形．

点评 本题考查了中点四边形、三角形的中位线定理、矩形的判定定理，掌握三角形的中位线平行于第三边，并且等于第三边的一半和四边相等的四边形是菱形、一个角是直角的平行四边形的矩形是解题的关键．