题目内容
8.某多边形所有内角的和与某一个外角的差是1710°,求这个多边形的边数与这个外角的度数.分析 根据n边形的内角和定理可知:n边形内角和为(n-2)×180°.设这个内角度数为x度,利用方程即可求出答案.
解答 解:设这个内角度数为x,根据题意,得
(n-2)×180°-(180-x)=1710°,
解得:x=1710°-180°n+540°=2250°-180°n,
由于0<x<180°,即0<2250°-180°n<180°,
解得11.5<n<12.5,
所以n=12.
故多边形的边数是12,
这个外角的度数为90°.
故答案为:12,90.
点评 本题主要考查了多边形的内角和定理.n边形的内角和为:180°•(n-2).

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
18. 小林去超市帮妈妈买回一批规格一样的花盆.如图,他把3个花盆叠在一起高度是9cm,把8个花盆叠在一起高度是14cm.若把100个花盆叠在一起时,它的高度约是( )
小林去超市帮妈妈买回一批规格一样的花盆.如图,他把3个花盆叠在一起高度是9cm,把8个花盆叠在一起高度是14cm.若把100个花盆叠在一起时,它的高度约是( )
 小林去超市帮妈妈买回一批规格一样的花盆.如图,他把3个花盆叠在一起高度是9cm,把8个花盆叠在一起高度是14cm.若把100个花盆叠在一起时,它的高度约是( )
小林去超市帮妈妈买回一批规格一样的花盆.如图,他把3个花盆叠在一起高度是9cm,把8个花盆叠在一起高度是14cm.若把100个花盆叠在一起时,它的高度约是( )| A. | 116cm | B. | 110cm | C. | 114cm | D. | 106cm |
18.如图所示,小刚手拿20元钱正在和售货员对话,请你仔细看图,1听果奶、1听可乐的单价分别是( )

| A. | 3元,3.5元 | B. | 3.5元,3元 | C. | 4元,4.5元 | D. | 4.5元,4元 |
 如图,已知等边△ABC,P为AC延长线上一点,以PA为边作等边△APE,EC延长线交BP于M,连接AM,求证:
如图,已知等边△ABC,P为AC延长线上一点,以PA为边作等边△APE,EC延长线交BP于M,连接AM,求证: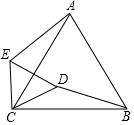 如图1,已知△ABC与△CDE均为等腰三角形,AC=BC,DC=EC,且∠ACB=∠DCE,连接AE、BD.
如图1,已知△ABC与△CDE均为等腰三角形,AC=BC,DC=EC,且∠ACB=∠DCE,连接AE、BD. 根据如图所示的程序计算函数值,若输入的x的值为-$\frac{5}{2}$,则输出y的值为-2.
根据如图所示的程序计算函数值,若输入的x的值为-$\frac{5}{2}$,则输出y的值为-2.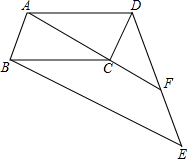 如图,四边形ABCD是平行四边形,连接AC并延长到点F,连接DF并延长到点E,使FE=DF,连接BE.
如图,四边形ABCD是平行四边形,连接AC并延长到点F,连接DF并延长到点E,使FE=DF,连接BE.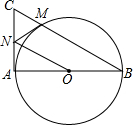 如图,在以AB为直径的⊙O中,过点A作⊙O的切线,点C为切线上一点,连接BC交⊙O于点M,过点M作⊙O的切线交AC于点N,连接ON.
如图,在以AB为直径的⊙O中,过点A作⊙O的切线,点C为切线上一点,连接BC交⊙O于点M,过点M作⊙O的切线交AC于点N,连接ON.