题目内容
20.在△ABC中,∠A=42°,高BE、CF所在的直线相交于点O,求∠BOC的度数.分析 作出图形,然后分①△ABC是锐角三角形时,根据直角三角形两锐角互余求出∠ABE,再根据三角形的一个外角等于与它不相邻的两个内角的和求解;②△ABC是钝角三角形时,根据对顶角相等可得∠ACF=∠OCE,再根据等角的余角相等可得∠BOC=∠A,③△ABC是直角三角形时,点C、O、E三点重合,∠BOC=0°.
解答  解:如图,①△ABC是锐角三角形时,
解:如图,①△ABC是锐角三角形时,
∵BE是高,
∴∠ABE=90°-∠A=90°-42°=48°,
在△BOF中,根据三角形的外角性质得,∠BOC=∠ABE+∠BFO=48°+90°=138°;
②△ABC是钝角三角形时,根据对顶角相等得,∠ACF=∠OCE,
∵BE、CF是高,
∴∠ACF+∠A=∠BOC+∠OCE=90°,
∴∠BOC=∠A=42°,
③△ABC是直角三角形时,点C、O、E三点重合,∠BOC=0°.
综上所述,∠BOC的度数是138°或42°或0°.
点评 本题考查了三角形的内角和定理,三角形的外角性质,难点在于本题没有明确△ABC的形状,应当注意需要分类讨论.

练习册系列答案
相关题目
5.近年来,随着我国国民经济的飞速发展,我国物流业的市场需求持续扩大,开封某物流公司承接A、B两种货物运输业务,5月份承接的A种货物和B种货物的数量与4月份相同,由于油价上涨等因素,5月份的运费单价在4月份的基础上进行了上调,下表是该公司4月份和5月份的货物运费清单;
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计6月份运输这种货物330吨,且A种货物的数量不大于B种货物的2倍,在运输单价与5月份相同的情况下,该物流公司6月份最多将收到多少运费?
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计6月份运输这种货物330吨,且A种货物的数量不大于B种货物的2倍,在运输单价与5月份相同的情况下,该物流公司6月份最多将收到多少运费?
| 货物运费单价(元/吨) | 当月运费总额/元 | ||
| A种货物 | B种货物 | ||
| 4月份 | 50 | 30 | 9500 |
| 5月份 | 70 | 40 | 13000 |
9.为了更好治理梅江河的水质,保护环境,宁都县治污公司决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如表:
经调查,购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a、b的值;
(2)经预算:宁都县治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案?
| A型 | B型 | |
| 价格(万元/台) | a | b |
| 处理污水量(吨/月) | 240 | 200 |
(1)求a、b的值;
(2)经预算:宁都县治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案?
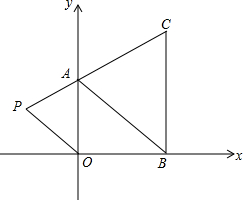 如图,在下面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,在第二象限内有一点P(m,$\frac{1}{2}$).
如图,在下面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,在第二象限内有一点P(m,$\frac{1}{2}$).