题目内容
17.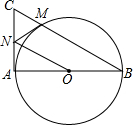 如图,在以AB为直径的⊙O中,过点A作⊙O的切线,点C为切线上一点,连接BC交⊙O于点M,过点M作⊙O的切线交AC于点N,连接ON.
如图,在以AB为直径的⊙O中,过点A作⊙O的切线,点C为切线上一点,连接BC交⊙O于点M,过点M作⊙O的切线交AC于点N,连接ON.(1)求证:MN=CN;
(2)若AB=2,填空:
①MN的延长线交BA延长线于点E,若ME=$\sqrt{3}$,则AC的长为$\frac{2\sqrt{3}}{3}$;
②当∠ABC的度数为45°时,四边形OBMN为平行四边形.
分析 (1)如图,连接OM,根据切线的性质得到∠OMN=90°,∠A=90°,根据余角的性质和等腰三角形的判定即可得到结论;
(2)①解直角三角形得到∠MOE=60°,根据外角的性质得到∠B=30°,于是得到结论;
②根据平行线的判定得到MN∥OB,由AN,MN是⊙O的切线,得到∠MNO=∠ANO,于是得到∠AON=∠MON=$\frac{1}{2}$∠AOM,推出∠AON=∠B,得到ON∥BC,即可得到结论.
解答 解:(1)如图,连接OM,
∵MN是⊙O的切线,
∴∠OMN=90°,
∵AC是⊙O的切线,
∴∠A=90°,
∴∠CMN+∠OMB=∠C+∠B=90°,
∵OM=OB,
∴∠OMB=∠B,
∴∠C=∠CMN,
∴MN=CN;
(2)①∵AB=2,
∴OM=1,
∵ME=$\sqrt{3}$,
∴tan∠MOE=$\sqrt{3}$,
∴∠MOE=60°,
∴∠B=30°,
∴AC=$\frac{\sqrt{3}}{3}$AB=$\frac{2\sqrt{3}}{3}$;
②当∠ABC的度数为45°时,四边形OBMN为平行四边形,
理由:∵∠ABC=45°,
∴∠C=45°,
∵CN=NM,
∴∠CMN=45°,
∴∠CNM=90°,
∴MN∥OB,
∵AN,MN是⊙O的切线,
∴∠MNO=∠ANO,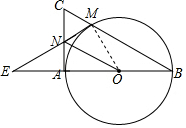
∵∠OMN=∠OAN=90°,
∴∠AON=∠MON=$\frac{1}{2}$∠AOM,
∵∠B=$\frac{1}{2}∠$AOM,
∴∠AON=∠B,
∴ON∥BC,
∴四边形OBMN为平行四边形.
故答案为:$\frac{2\sqrt{3}}{3}$,45°.
点评 本题考查了切线的性质,平行四边形的判定和性质,解直角三角形,正确的理解题意是解题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
5.近年来,随着我国国民经济的飞速发展,我国物流业的市场需求持续扩大,开封某物流公司承接A、B两种货物运输业务,5月份承接的A种货物和B种货物的数量与4月份相同,由于油价上涨等因素,5月份的运费单价在4月份的基础上进行了上调,下表是该公司4月份和5月份的货物运费清单;
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计6月份运输这种货物330吨,且A种货物的数量不大于B种货物的2倍,在运输单价与5月份相同的情况下,该物流公司6月份最多将收到多少运费?
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计6月份运输这种货物330吨,且A种货物的数量不大于B种货物的2倍,在运输单价与5月份相同的情况下,该物流公司6月份最多将收到多少运费?
| 货物运费单价(元/吨) | 当月运费总额/元 | ||
| A种货物 | B种货物 | ||
| 4月份 | 50 | 30 | 9500 |
| 5月份 | 70 | 40 | 13000 |
9.为了更好治理梅江河的水质,保护环境,宁都县治污公司决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如表:
经调查,购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a、b的值;
(2)经预算:宁都县治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案?
| A型 | B型 | |
| 价格(万元/台) | a | b |
| 处理污水量(吨/月) | 240 | 200 |
(1)求a、b的值;
(2)经预算:宁都县治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案?
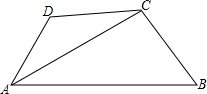 如图所示,在四边形ABCD中,AC平分∠BAD,∠ADC+∠ABC=180°.
如图所示,在四边形ABCD中,AC平分∠BAD,∠ADC+∠ABC=180°.