题目内容
16.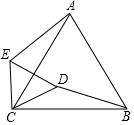 如图1,已知△ABC与△CDE均为等腰三角形,AC=BC,DC=EC,且∠ACB=∠DCE,连接AE、BD.
如图1,已知△ABC与△CDE均为等腰三角形,AC=BC,DC=EC,且∠ACB=∠DCE,连接AE、BD.(1)求证:△BCD≌△ACE;
(2)如图2,若DC⊥EC,试判断直线AE与直线BD的位置关系,并说明理由.
分析 (1)证出∠BCD=∠ACE,由SAS证明△BCD≌△ACE即可;
(2)延长BD交AE于M,交AC于N,由全等三角形的性质得出∠CBD=∠CAE,由直角三角形的性质和对顶角相等证出∠CAE+∠ANM=90°,由三角形内角和定理得出∠AMN=90°即可.
解答 (1)证明:∵∠ACB=∠DCE,
∴∠ACB-∠ACD=∠DCE-∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中,$\left\{\begin{array}{l}{BC=AC}&{\;}\\{∠BCD=∠ACE}&{\;}\\{DC=EC}&{\;}\end{array}\right.$,
∴△BCD≌△ACE(SAS);
(2)解:直线AE⊥直线BD;理由如下: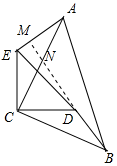
延长BD交AE于M,交AC于N,如图所示:
∵△BCD≌△ACE,
∴∠CBD=∠CAE,
∵DC⊥EC,
∴∠DCE=90°,
∴∠ACB=90°,
∴∠CBD+∠BNC=90°,
∵∠BNC=∠ANM,
∴∠CAE+∠ANM=90°,
∴∠AMN=90°,
∴AE⊥BD.
点评 本题考查了全等三角形的判定与性质、直角三角形的性质、对顶角相等的性质、等腰三角形的性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
5.近年来,随着我国国民经济的飞速发展,我国物流业的市场需求持续扩大,开封某物流公司承接A、B两种货物运输业务,5月份承接的A种货物和B种货物的数量与4月份相同,由于油价上涨等因素,5月份的运费单价在4月份的基础上进行了上调,下表是该公司4月份和5月份的货物运费清单;
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计6月份运输这种货物330吨,且A种货物的数量不大于B种货物的2倍,在运输单价与5月份相同的情况下,该物流公司6月份最多将收到多少运费?
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计6月份运输这种货物330吨,且A种货物的数量不大于B种货物的2倍,在运输单价与5月份相同的情况下,该物流公司6月份最多将收到多少运费?
| 货物运费单价(元/吨) | 当月运费总额/元 | ||
| A种货物 | B种货物 | ||
| 4月份 | 50 | 30 | 9500 |
| 5月份 | 70 | 40 | 13000 |
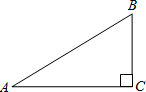 如图,在Rt△ABC中,∠ACB=90°,用尺规在BC边上找一点O,使得以点O为圆心,OC为半径的圆与AB相切,并画出⊙O(保留作图痕迹,不写作法)
如图,在Rt△ABC中,∠ACB=90°,用尺规在BC边上找一点O,使得以点O为圆心,OC为半径的圆与AB相切,并画出⊙O(保留作图痕迹,不写作法) 如图,7个大小、形状完全相同的小长方形组成1个周长为68的大长方形,则大长方形的面积为280.
如图,7个大小、形状完全相同的小长方形组成1个周长为68的大长方形,则大长方形的面积为280.