如图.⊙O的直径为10.弦AB长为8.点P在AB上运动.则OP的最小值是3．题目和参考答案——青夏教育精英家教网—

题目内容

16．

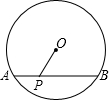如图，⊙O的直径为10，弦AB长为8，点P在AB上运动，则OP的最小值是3．

分析根据“点到直线的最短距离是垂线段的长度”知当OP⊥AB时，OP的值最小．连接OA，在直角三角形OAP中由勾股定理即可求得OP的长度．

解答解：当OP⊥AB时，OP的值最小，
则AP′=BP′=$\frac{1}{2}$AB=4，
如图所示，连接OA，
在Rt△OAP′中，AP′=4，OA=5，
则根据勾股定理知OP′=3，即OP的最小值为3．

点评本题主要考查了勾股定理、垂径定理．注意两点之间，垂线段最短是解答此题的关键．

练习册系列答案

相关题目

9．如果一个多边形的内角和是其外角和的两倍，那么这个多边形是（　　）

8．一组数据：5，7，4，9，7的中位数和众数分别是（　　）

4．若2y^m+5xⁿ⁺³与-3x³y²是同类项，则mⁿ=1．

11．如图1，将三角板ABC与三角板ADE摆放在一起；如图2，其中∠ACB=30°，∠DAE=45°∠BAC=∠D=90°．固定三角板ABC，将三角板ADE绕点A按顺时针方向旋转，记旋转角∠CAE=α（0°＜α＜180°）．
（1）当α为15度时，AD∥BC，并在图3中画出相应的图形；
（2）当△ADE 的一边与△ABC的某一边平行（不共线）时，写出旋转角 α的所有可能的度数；
（3）当0°＜α＜45°时，连结BD，利用图4探究∠BDE+∠CAE+∠DBC值的大小变化情况，并给出你的证明．

1．（1）请写出是旋转对称图形的两种多边形（正三角形除外）的名称，并分别写出其旋转角α的最小值；
（2）下面的网格图都是由边长为1的正三角形组成的，请以图中给出的图案为基本图形（其顶点均在格点上），在图2、图3中再分别添加若干个基本图形，使添加的图形与原基本图形组成一个新图案，要求：
①图2中设计的图案既是旋转对称图形又是轴对称图形；
②图3中设计的图案是旋转对称图形，但不是中心对称图形；
③所设计的图案顶点都在格点上，并给图案上阴影（建议用一组平行线段表示阴影）．

8．

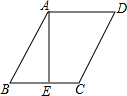如图，在平行四边形ABCD中，AE⊥BC于E，AE=EB=EC=a，且a是一元二次方程x²+2x-3=0的根，则平行四边形ABCD的周长为（　　）

5．已知：在△ABC中，点D为AB上一点，连接CD，∠ADC的平分线交AC于点E，过点E作CD、AB的平行线，分别交AB、CD、BC于点F、M、N．
（1）如图l，求证：四边形DFEM为菱形；
（2）如图2，∠ACB=90°，点D为边AB的中点，连接DN、MF．在不添加任何辅助线的情况下，请直接写出图2中的所有平行四边形（不包括以DF为一边的平行四边形）．

4．判断关于x的一元二次方程kx²+2（k+1）x+k+2=0的根的情况，结论是有两不相等的实数根．（填“有两个不相等的实数根”、“有两个相等的实数根”或“没有实数根”）

试题分类