题目内容
4．判断关于x的一元二次方程kx2+2（k+1）x+k+2=0的根的情况，结论是有两不相等的实数根．（填“有两个不相等的实数根”、“有两个相等的实数根”或“没有实数根”）分析 根据根的判别式可得△=4（k+1）2-4k（k+2）=4＞0，据此判断方程有两个不相等的实数根．
解答 解：∵一元二次方程kx2+2（k+1）x+k+2=0，
∴△=4（k+1）2-4k（k+2）=4
∴△＞0，
∴此方程有两不相等实数根，
故答案为：有两个不相等的实数根．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
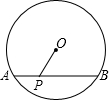如图，⊙O的直径为10，弦AB长为8，点P在AB上运动，则OP的最小值是3．
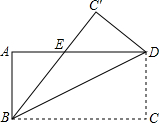如图，已知矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于E，AD=8，AB=4，则DE的长为（ ）
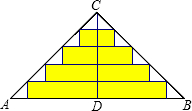如图，△ABC是一张直角三角形彩色纸，AC=15cm，BC=20cm．若将斜边上的高CD 分成n等分，然后裁出（n-1）张宽度相等的长方形纸条．则这（n-1）张纸条的面积和是$\frac{150（n-1）}{n}$cm2．
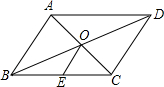如图，在平行四边形ABCD中，点E是BC的中点，∠BOE=30°，OD=2，cos∠ADB=$\frac{{\sqrt{3}}}{2}$．则CD=$\frac{4\sqrt{3}}{3}$．
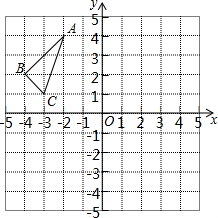△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．
