题目内容
8.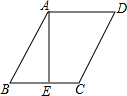 如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )
如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )| A. | $12-6\sqrt{2}$ | B. | $6\sqrt{2}+12$ | C. | $4+2\sqrt{2}$ | D. | $4-2\sqrt{2}$ |
分析 先解方程求得a,再根据勾股定理求得AB,从而计算出?ABCD的周长即可.
解答 解:∵a是一元二次方程x2+2x-3=0的根,
∴(x-1)(x+3)=0,
即x=1或-3,
∵AE=EB=EC=a,
∴a=1,
在Rt△ABE中,AB=$\sqrt{{a}^{2}+{a}^{2}}=\sqrt{2}a=\sqrt{2}$,
∴?ABCD的周长=4a+2$\sqrt{2}$a=4+2$\sqrt{2}$.
故选C.
点评 本题考查了用因式分解法解一元二次方程,以及平行四边形的性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
1. 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若S△ADE:S△ABC=4:9,则AD:AB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若S△ADE:S△ABC=4:9,则AD:AB=( )
 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若S△ADE:S△ABC=4:9,则AD:AB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若S△ADE:S△ABC=4:9,则AD:AB=( )| A. | 1:2 | B. | 2:3 | C. | 1:3 | D. | 4:9 |
13.-2015的相反数为( )
| A. | -2015 | B. | $\frac{1}{2015}$ | C. | 2015 | D. | ±2015 |
 B.
B.  C.
C.  D.
D. 
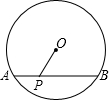 如图,⊙O的直径为10,弦AB长为8,点P在AB上运动,则OP的最小值是3.
如图,⊙O的直径为10,弦AB长为8,点P在AB上运动,则OP的最小值是3. 由几个大小相同的正方体组成的几何体如图所示,则它的俯视图为( )
由几个大小相同的正方体组成的几何体如图所示,则它的俯视图为( )



 如图,等腰三角形ABC的周长为21,底边BC的长为5,腰AB的垂直平分线交AB于点D,交AC于点E,连接BE,则三角形BEC的周长为( )
如图,等腰三角形ABC的周长为21,底边BC的长为5,腰AB的垂直平分线交AB于点D,交AC于点E,连接BE,则三角形BEC的周长为( )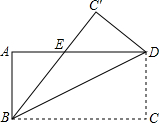 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为( )
如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为( )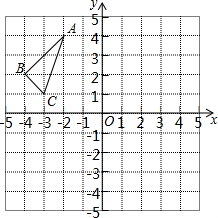 △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.