��Ŀ����
4�� ��ͼ���ڵ�������ABCD�У�AD��BC��AB=DC=5��AD=6��BC=12����P�ӵ�B���������߶�BA-AD-DC��ÿ��1����λ�����ٶ����C�����˶�����Q�ӵ�C�������߶�CB������ÿ��$\frac{3}{5}$����λ�����ٶ������˶�������Q����������QK��BC�������߶�CD-DA-AB�ڵ�E����P��Qͬʱ��ʼ�˶�������P���C�غ�ʱֹͣ�˶�����QҲ��ֹ֮ͣ����P��Q�˶���ʱ��Ϊt�루t��0����
��ͼ���ڵ�������ABCD�У�AD��BC��AB=DC=5��AD=6��BC=12����P�ӵ�B���������߶�BA-AD-DC��ÿ��1����λ�����ٶ����C�����˶�����Q�ӵ�C�������߶�CB������ÿ��$\frac{3}{5}$����λ�����ٶ������˶�������Q����������QK��BC�������߶�CD-DA-AB�ڵ�E����P��Qͬʱ��ʼ�˶�������P���C�غ�ʱֹͣ�˶�����QҲ��ֹ֮ͣ����P��Q�˶���ʱ��Ϊt�루t��0������1������P�˶���AD��ʱ��tΪ��ֵʱ��ʹPQ��DC��
��2��������QKɨ������ABCD�����Ϊs����s��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3���������˶������У���PDQ�ܷ���ֱ�������Σ����ܣ�ֱ��д����ʱt��ֵ��
���� ��1������ƽ���ı��ε����ʣ��ɵ�PD��QC�Ĺ�ϵ���ɵù���t�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��2���������ۣ�0��t��5�����������ε������ʽ���ɵô𰸣�5��t��15ʱ���������ε������ʽ���ɵô𰸣�15��t��16ʱ������ͼ�θ�����ɵ��������Σ��������ε������ʽ���ɵô𰸣�
��3���������ۣ���PDC=90�����P��A�غ�ʱ���ɵ�t��ֵ����PDQ=90��ʱ���ɵ�PD=QF�����ݽⷽ�̣��ɵô𰸣�
��� �⣺��1����ͼ1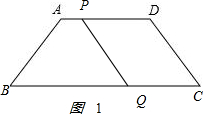 ��
��
?PD=AB+AD=5+6=11��BP=t��PD=11-t��CQ=$\frac{3}{5}$t��
��PQ��CD��PD��CQ��
��PD=CQ����$\frac{3}{5}$t=11-t��
���t=$\frac{55}{8}$���룩��
����P�˶���AD��ʱ��t=$\frac{55}{8}$ʱ��ʹPQ��DC��
��2����ͼ2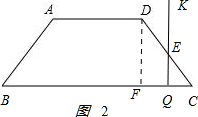 ��
��
��0��t��5ʱ��CQ=$\frac{3}{5}$t��FC=$\frac{BC-AD}{2}$=3���ɹ��ɶ�������FD=4��
��QE��DF��
���CQE�ס�CFD��$\frac{QE}{FD}$=$\frac{CQ}{CF}$��
���CQ=$\frac{4}{5}$t��
S=$\frac{1}{2}$CQ•QE=$\frac{1}{2}$��$\frac{3}{5}$t��$\frac{4}{5}$t=$\frac{6}{25}$t2��
��ͼ3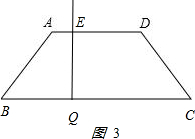 ��
��
5��t��15ʱ��S=$\frac{1}{2}$��$\frac{3}{5}$t-3+$\frac{3}{5}$t����4=$\frac{12}{5}$t-6��
��ͼ4��15��t��16ʱ��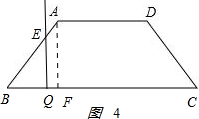 ��
��
BQ=12-$\frac{3}{5}$t��QF=QC-CF=$\frac{3}{5}$t-9��
��BEQ�ס�BFA��
$\frac{EQ}{AF}$=$\frac{BQ}{BF}$�����EQ=16-$\frac{4}{5}$t��
s=$\frac{1}{2}$��16-4t+4����$\frac{3}{5}$t-9��+$\frac{1}{2}$��3+9����4=-$\frac{6}{5}$t2+24t-56��
��3����PDQ����ֱ�������Σ��������£�
�ٵ���PDQ=90��ʱ��BP=5t=5��CQ=$\frac{3}{5}$t=3��
���t=5��
�ڵ���QPD=90��ʱ��ͼ5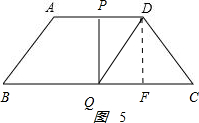 ��PD=11-t��QE=$\frac{3}{5}$t-3��
��PD=11-t��QE=$\frac{3}{5}$t-3��
PDFQ�Ǿ��Σ�PD=EQ����11-t=$\frac{3}{5}$t-3��
���t=$\frac{35}{4}$��
����������t=5��t=$\frac{35}{4}$ʱ����PDQ�ܷ���ֱ�������Σ�
���� ���⿼�����ı����ۺ��⣬��1��������ƽ���ı��ε����ʵó�����t�ķ����ǽ���ؼ�����2�����������ǽ���ؼ��������������ε������ʽ�����ε������ʽ����3���������ۣ���PDC=90�����P��A�غ�ʱ���ɵ�t��ֵ����PDQ=90��ʱ���ɵ�PD=QF��������t�ķ��̣�

 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�| A�� | 1 | B�� | -1 | C�� | 2 | D�� | -2 |
| A�� | -$\sqrt{2}$ | B�� | $\sqrt{2}$ | C�� | $\frac{1}{\sqrt{2}}$ | D�� | 2 |
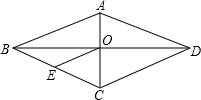 ��֪����ͼ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��OE��DC��BC�ڵ�E��AD=6cm����OE�ij�Ϊ��������
��֪����ͼ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��OE��DC��BC�ڵ�E��AD=6cm����OE�ij�Ϊ��������| A�� | 6cm | B�� | 4cm | C�� | 3cm | D�� | 2cm |
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 1 |
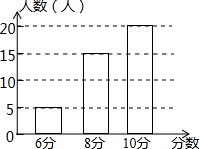 ��һ���������ϣ�������ʦ�Ծ��꼶һ���40��ͬѧ������������Զ��Ŀ�IJ��ԣ��������÷�������Ӧ��������ͼ��ʾ����β��Ե�ƽ����Ϊ8.75�֣�
��һ���������ϣ�������ʦ�Ծ��꼶һ���40��ͬѧ������������Զ��Ŀ�IJ��ԣ��������÷�������Ӧ��������ͼ��ʾ����β��Ե�ƽ����Ϊ8.75�֣�