题目内容
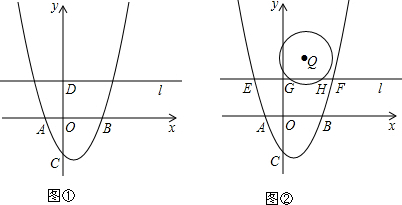
9.如图①,抛物线y=ax2+bx+c经过A(-1,0)、B(2,0)、C(0,-2)三点.直线l:y=m(m>0)与y轴交于D.(Ⅰ)求抛物线方程;
(Ⅱ)直线l上是否存在点P,使得以P、O、D为顶点的三角形与△AOC全等?若存在,求出点P的坐标;若不存在,请说明理由.
(Ⅲ)如图②,以点Q(1,3)为圆心,$\sqrt{2}$为半径作圆Q.若直线l与抛物线交于E、F两点,与圆Q交于G、H两点,且EG+FH=$\frac{3}{2}$GH,试求m的值.
分析 (I)先把A、B、C三点坐标代入抛物线y=ax2+bx+c,求出a、b、c的值,进而可得出其抛物线方程;
(II)假设存在点P,使得以P、O、D为顶点的三角形与△AOC全等,由已知OA=1,OC=2,D(0,m)(m>0),设P(p,m).根据点P在直线l上可知PD⊥OD,∠PDO=∠AOC=90°.再分△PDO≌△AOC,△ODP≌△AOC两种情况求出P点坐标即可;
(III)过Q作QM⊥GH于M,连接QH,根据EG+FH=$\frac{3}{2}$GH可得出EF的长,故QM=|3-m|,根据垂径定理可得GH的表达式,当y=x2-x-2=m时求出x的值,故可得出即E,F的坐标,根据两点间的距离公式求出EF的长,代入①是即可得出结论.
解答 解:(Ⅰ)∵依题意得:$\left\{\begin{array}{l}a-b+c=0\\ 4a+2b+c=0\\ c=-2\end{array}\right.$
解得$\left\{\begin{array}{l}a=1\\ b=-1\\ c=-2\end{array}\right.$,
∴抛物线方程为y=x2-x-2;
(Ⅱ)假设存在点P,使得以P、O、D为顶点的三角形与△AOC全等,
由已知OA=1,OC=2,D(0,m)(m>0),设P(p,m).
∵点P在直线l:y=m上,
∴PD⊥OD,∠PDO=∠AOC=90°.
①若△PDO≌△AOC,
则PD=|p|=OA=1,OD=m=OC=2,
∴P点的坐标为(-1,2)或(1,2);
②若△ODP≌△AOC,
则PD=|p|=OC=2,OD=m=OA=1.
∴P点的坐标为(-2,1)或(2,1).
综上满足条件的点P存在,其坐标可能为(-2,1)、(-1,2)、(1,2)、(2,1).
(Ⅲ)过Q作QM⊥GH于M,连接QH,
∵EG+FH=$\frac{3}{2}$GH,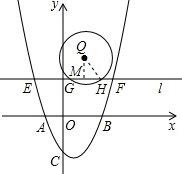
∴EG+GH+FH=$\frac{3}{2}$GH+GH+$\frac{5}{2}$GH,即EF=$\frac{5}{2}$GH①.
∵QM=|3-m|,
由垂径定理可得GH=2$\sqrt{{QH}^{2}-{QM}^{2}}$=2$\sqrt{2-|3-m{|}^{2}}$=2$\sqrt{6m-7-{m}^{2}}$
当y=x2-x-2=m,
解得x1=$\frac{1-\sqrt{4m+9}}{2}$,x2=$\frac{1+\sqrt{4m+9}}{2}$,
即E($\frac{1-\sqrt{4m+9}}{2}$,m),F($\frac{1+\sqrt{4m+9}}{2}$,m),
∴EF=$\sqrt{4m+9}$(求EF的长用韦达定理也可以)
代入①式得$\sqrt{4m+9}$=$\frac{5}{2}$×2$\sqrt{2-|3-m{|}^{2}}$=5$\sqrt{6m-7-{m}^{2}}$,两边平方整理得25m2-146m+184=0,解得m=$\frac{46}{25}$或4.
点评 本题考查的是二次函数综合题,涉及到待定系数法求二次函数的解析式、全等三角形的判定与性质、垂径定理及勾股定理等知识,难度适中.

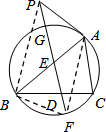 如图,△ABC内接于⊙O,过BC的中点D作直线l∥AC,l与AB交于点E,与⊙O交于点G、F,与⊙O在点A处的切线交于点P,若PE=3,ED=2,EF=3,则PA的长度为( )
如图,△ABC内接于⊙O,过BC的中点D作直线l∥AC,l与AB交于点E,与⊙O交于点G、F,与⊙O在点A处的切线交于点P,若PE=3,ED=2,EF=3,则PA的长度为( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
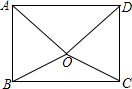 如图,点O为矩形ABCD内的一点,OB=OC,求证:OA=OD.
如图,点O为矩形ABCD内的一点,OB=OC,求证:OA=OD.
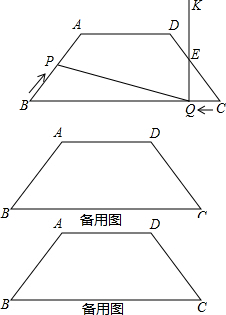 如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12,点P从点B出发沿折线段BA-AD-DC以每秒1个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒$\frac{3}{5}$个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E;点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止,设P、Q运动的时间为t秒(t>0).
如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12,点P从点B出发沿折线段BA-AD-DC以每秒1个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒$\frac{3}{5}$个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E;点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止,设P、Q运动的时间为t秒(t>0). 由图中所表示的已知角的度数,可知∠α的度数为50°.
由图中所表示的已知角的度数,可知∠α的度数为50°.