题目内容
7.某厂制作甲、乙两种环保包装盒,已知同样用6m材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制成一个乙盒需要多用20%的材料.(1)求制作每个甲盒、乙盒各用多少米材料?
(2)如果制作甲、乙两种包装盒共3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需要材料的总长度l(m)与甲盒数量n(个)之间的函数关系式,并求出最少需要多少米材料?
分析 (1)设制作每个乙盒用x米材料,则制作甲盒用(1+20%)x米材料,根据“同样用6m材料制成甲盒的个数比制成乙盒的个数少2个”,列出方程,即可解答;
(2)根据所需要材料的总长度l=甲盒材料的总长度+乙盒材料的总长度,列出函数关系式;再根据“甲盒的数量不少于乙盒数量的2倍”求出n的取值范围,根据一次函数的性质,即可解答.
解答 解:(1)设制作每个乙盒用x米材料,则制作甲盒用(1+20%)x米材料,
$\frac{6}{x}-2=\frac{6}{(1+20%)x}$,
解得:x=0.5,
经检验x=0.5是原方程的解,
∴(1+20%)x=0.6(米),
答:制作每个甲盒用0.6米材料;制作每个乙盒用0.5米材料.
(2)根据题意得:l=0.6n+0.5(3000-n)=0.1n+1500,
∵甲盒的数量不少于乙盒数量的2倍,
∴n≥2(3000-n)
解得:n≥2000,
∴2000≤n<3000,
∵k=0.1>0,
∴l随n增大而增大,
∴当n=2000时,l最小1700米.
点评 本题考查了一次函数的应用,解决本题的关键是利用一次函数的性质解决实际问题.

练习册系列答案
相关题目
18.2015年中国高端装备制造业销售收入将超6万亿元,其中6万亿元用科学记数法可表示为( )
| A. | 0.6×1013元 | B. | 60×1011元 | C. | 6×1012元 | D. | 6×1013元 |
15. 如图,数轴上所表示关于x的不等式组的解集是( )
如图,数轴上所表示关于x的不等式组的解集是( )
 如图,数轴上所表示关于x的不等式组的解集是( )
如图,数轴上所表示关于x的不等式组的解集是( )| A. | x≥2 | B. | x>2 | C. | x>-1 | D. | -1<x≤2 |
11.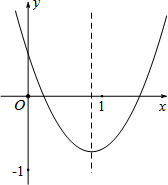 已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2-4ac,a+b+c,a-b+c,2a+b中,其值为正的式子的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2-4ac,a+b+c,a-b+c,2a+b中,其值为正的式子的个数为( )
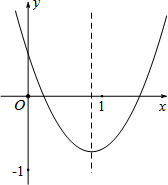 已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2-4ac,a+b+c,a-b+c,2a+b中,其值为正的式子的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2-4ac,a+b+c,a-b+c,2a+b中,其值为正的式子的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 4个以上 |
9.已知直线y=-x+6和y=x-2,则它们与y轴所围成的三角形的面积为( )
| A. | 6 | B. | 10 | C. | 16 | D. | 12 |
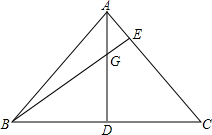 已知,AD⊥BC于点D,AD=BD,BE⊥AC于点E,BE交AD于点G,请说明:BG=AC.
已知,AD⊥BC于点D,AD=BD,BE⊥AC于点E,BE交AD于点G,请说明:BG=AC.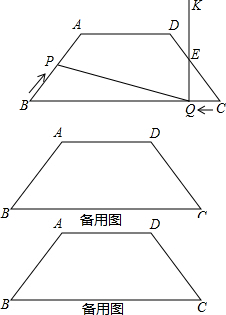 如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12,点P从点B出发沿折线段BA-AD-DC以每秒1个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒$\frac{3}{5}$个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E;点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止,设P、Q运动的时间为t秒(t>0).
如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12,点P从点B出发沿折线段BA-AD-DC以每秒1个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒$\frac{3}{5}$个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E;点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止,设P、Q运动的时间为t秒(t>0).