题目内容
11.计算或解方程:①(4$\sqrt{6}$-4$\sqrt{\frac{1}{2}}$+3$\sqrt{8}$)÷2$\sqrt{2}$
②3($\sqrt{3}$-π)0-$\frac{\sqrt{20}-\sqrt{15}}{\sqrt{5}}$+(-1)2011
③2x2-4x-1=0(配方法)
④2(x-3)2=x(x-3)
分析 ①根据二次根式的混合运算计算即可;
②根据零指数和二次根式的四则运算计算即可;
③解题时要注意解题步骤的准确应用,把左边配成完全平方式,右边化为常数;
④先把右边的项移到左边,按解一元二次方程的解法-因式分解法计算即可.
解答 解:①(4$\sqrt{6}$-4$\sqrt{\frac{1}{2}}$+3$\sqrt{8}$)÷2$\sqrt{2}$
=2$\sqrt{3}$-1+$\sqrt{3}$
=3$\sqrt{3}$-1;
②3($\sqrt{3}$-π)0-$\frac{\sqrt{20}-\sqrt{15}}{\sqrt{5}}$+(-1)2011
=1-2+$\sqrt{3}$-1
=$\sqrt{3}$-2;
③2x2-4x-1=0(配方法)
2(x2-2x-$\frac{1}{2}$)=0,
(x-1)2=$\frac{3}{2}$,
∴x-1=$\frac{\sqrt{6}}{2}$,或x-1=-$\frac{\sqrt{6}}{2}$,
∴x1=$\frac{2+\sqrt{6}}{2}$,x2=$\frac{2-\sqrt{6}}{2}$;
④2(x-3)2=x(x-3),
(x-3)(x-6)=0,
∴x-3=0,或x-6=0,
∴x1=3,x2=6.
点评 本题考查了二次根式的混合运算,零指数幂,配方法和因式分解法解一元二次方程,熟记解方程的方法是解题的关键.

练习册系列答案
相关题目
16.已知P(m-1,2-m)在第一象限,则m的取值范围为( )
| A. | $\frac{1}{2}$<m<2 | B. | 1<m<2 | C. | m<2 | D. | m>$\frac{1}{2}$ |
3.某市电力公司为了鼓励居民节约用电,采用分段计费的方法计算电费:每月用电不超过100度时,按每度0.37元计费;每月用电超过100度时,其中超过部分按每度0.50元计费.
(1)用电x度时,应交电费y元,当x≤100和x>100时,分别写出y关于x的关系式.
(2)小王家第一季度交纳电费如下:
问小王家第一季度共用电多少度?
(1)用电x度时,应交电费y元,当x≤100和x>100时,分别写出y关于x的关系式.
(2)小王家第一季度交纳电费如下:
| 月 份 | 一月份 | 二月份 | 三月份 | 四月份 |
| 交费金额 | 76元 | 63元 | 45元6角 | 184元6角 |
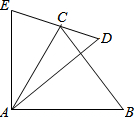 如图所示,AE=AC,AD=AB,∠EAC=∠DAB,求证:∠D=∠B.
如图所示,AE=AC,AD=AB,∠EAC=∠DAB,求证:∠D=∠B.