题目内容
 已知:如图,一次函数y=x+2的图象与反比例函数y=
已知:如图,一次函数y=x+2的图象与反比例函数y=| k |
| x |
(1)求反比例函数y=
| k |
| x |
(2)点C(n,1)在反比例函数y=
| k |
| x |
(3)在x轴上找出点P,使△ABP是以AB为斜边的直角三角形,请直接写出所有符合条件的点P的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先求得A的坐标,然后利用待定系数法即可求得反比例函数y=
的表达式;
(2)把C(n,1)(1)求得的解析式就可求得C的坐标,根据梯形公式即可求得△AOC的面积;
(3)联立方程求得B的坐标,设P(x,0),根据勾股定理列出式子,解方程即可求得P的坐标.
| k |
| x |
(2)把C(n,1)(1)求得的解析式就可求得C的坐标,根据梯形公式即可求得△AOC的面积;
(3)联立方程求得B的坐标,设P(x,0),根据勾股定理列出式子,解方程即可求得P的坐标.
解答:解:(1)∵点A(1,m)在一次函数y=x+2的图象上,
∴m=3.
∴点A的坐标为(1,3).
∵点A(1,3)在反比例函数y=
的图象上,
∴k=3.
∴反比例函数y=
的表达式为y=
.
(2)∵点C(n,1)在反比例函数y=
的图象上,
∴n=3.
∴C(3,1).
∵A(1,3),
∴S△AOC=
×(1+3)×(3-1)=4.
(3)解
得
,
,
∴A(1,3),B(-3,-1),
设P(x,0),
根据题意:(x-1)2+32+(x+3)2+12=(1+3)2+(3+1)2
整理得:x2+2x-6=0,
解得:x1=-
-1,x2=
-1,
∴所有符合条件的点P的坐标:P1(-
-1,0),P2(
-1,0).
∴m=3.
∴点A的坐标为(1,3).
∵点A(1,3)在反比例函数y=
| k |
| x |
∴k=3.
∴反比例函数y=
| k |
| x |
| 3 |
| x |
(2)∵点C(n,1)在反比例函数y=
| 3 |
| x |
∴n=3.
∴C(3,1).
∵A(1,3),
∴S△AOC=
| 1 |
| 2 |
(3)解
|
|
|
∴A(1,3),B(-3,-1),
设P(x,0),
根据题意:(x-1)2+32+(x+3)2+12=(1+3)2+(3+1)2
整理得:x2+2x-6=0,
解得:x1=-
| 7 |
| 7 |
∴所有符合条件的点P的坐标:P1(-
| 7 |
| 7 |
点评:本题考查了反比例函数和一次函数的交点问题,应用的知识点有:待定系数法求解析式,三角形的面积,勾股定理等.

练习册系列答案
相关题目
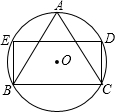 如图,△ABC是⊙O的内接等边三角形,AB=1.点D,E在圆上,四边形BCDE为矩形,则这个矩形的面积是( )
如图,△ABC是⊙O的内接等边三角形,AB=1.点D,E在圆上,四边形BCDE为矩形,则这个矩形的面积是( )A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
 如图,已知在Rt△ABC中,∠ACB=90°,点D在AB上,CD=5,AC=8,sin∠ACD=
如图,已知在Rt△ABC中,∠ACB=90°,点D在AB上,CD=5,AC=8,sin∠ACD=