题目内容
1．用配方法解方程x2+6x-15=0时，原方程应变形为（ ）| A． | （x+3）2=24 | B． | （x-3）2=6 | C． | （x+3）2=6 | D． | （x-3）2=24 |
分析 把常数项-15移项后，应该在左右两边同时加上一次项系数6的一半的平方．
解答 解：移项得，x2+6x=15，
配方得，x2+6x+9=15+9，
即（x+3）2=24，
故选A．
点评 本题考查了解一元二次方程，配方法的一般步骤：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方．选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
练习册系列答案
相关题目
11．
如图，在?ABCD中，若M为BC边的中点，AM与BD交于点N，那么S△BMN：S?ABCD=（ ）
如图，在?ABCD中，若M为BC边的中点，AM与BD交于点N，那么S△BMN：S?ABCD=（ ）| A． | 1：12 | B． | 1：9 | C． | 1：8 | D． | 1：6 |
12．下列方程是一元一次方程的有（ ）
x2+3x=2；x+1=y-2；$\frac{1}{7}$x-3=$\frac{3}{5}$；x+$\frac{1}{x}$=2．
x2+3x=2；x+1=y-2；$\frac{1}{7}$x-3=$\frac{3}{5}$；x+$\frac{1}{x}$=2．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
9．
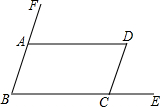如图，在平行四边形ABCD中，点E、F分别在BC、BA的延长线上，∠DCE=65°，则∠FAD的大小是（ ）
如图，在平行四边形ABCD中，点E、F分别在BC、BA的延长线上，∠DCE=65°，则∠FAD的大小是（ ）| A． | 115° | B． | 25° | C． | 65° | D． | 35° |
16．下列方程是一元二次方程的是（ ）
| A． | x-3=2x | B． | x2-2=0 | C． | x2-2y=1 | D． | $\frac{1}{x}+1=2x$ |
6．当k不大于6$\frac{1}{4}$时，方程（k-4）x2-（2k-5）x+k=0的解的情况是（ ）
| A． | 有两个不相等的实根 | B． | 有两个相等的实根 | ||
| C． | 有两个实数根 | D． | 以上结论都不对 |
如图，在Rt△ABC中，∠BAC=90°，延长BA到点D，使AD等于二分之一AB，点E，F分别为BC，AC的中点．
10．若x=0的方程3x-2m=1的解，则m的值是（ ）
| A． | -$\frac{1}{2}$ | B． | 2 | C． | -2 | D． | 0 |