题目内容
16.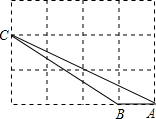 如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )
如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
分析 根据勾股定理,可得AC的长,根据锐角三角函数的正弦等于对边比斜边,可得答案.
解答 解:如图: ,
,
由勾股定理,得
AC=$\sqrt{C{D}^{2}+A{D}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
由锐角三角函数的正弦等于对边比斜边,得
sinA=$\frac{CD}{AC}$=$\frac{2}{2\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
故选:D.
点评 本题考查了锐角三角函数的定义,先求斜边,再求锐角三角函数的正弦.

练习册系列答案
相关题目
1.若a:b=3:5,且b是a、c的比例中项,那么b:c的值是( )
| A. | 3:2 | B. | 5:3 | C. | 3:5 | D. | 2:3 |
5.小明同学在期中考试中,数学、语文的平均分是95分,而数学、语文、英语三科平均分不低于98分,则小明同学的英语成绩至少为( )
| A. | 96分 | B. | 98分 | C. | 100分 | D. | 104分 |
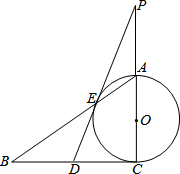 如图,Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点E,D是BC的中点,DE的延长线交CA的延长线于点P.
如图,Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点E,D是BC的中点,DE的延长线交CA的延长线于点P.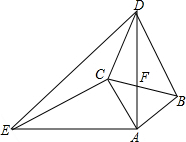 如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.