题目内容
 如图,在等腰梯形ABCD中,已知AD∥BC,AD=AB,AB⊥AC,求∠B的度数.
如图,在等腰梯形ABCD中,已知AD∥BC,AD=AB,AB⊥AC,求∠B的度数.考点:等腰梯形的性质
专题:
分析:首先设∠CAD=x°,由AB=AD=CD,AD∥BC,可求得∠ACD=∠CAD=∠ACB=x°,∠B=∠BCD=2x°,然后由∠ACB+∠B=90°,可得方程:x+2x=90,解此方程即可求得答案.
解答:解:设∠CAD=x°,
∵等腰梯形ABCD中,AB=CD,
又AB=AD,
∴AD=CD,
∴∠ACD=∠CAD=x°.
∵AD∥BC,
∴∠CAD=∠ACB=x°.
∵等腰梯形ABCD中,AB=CD,
∴∠B=∠BCD=2x°.
∵在△ABC中,AB⊥AC,
∴∠ACB+∠B=90°,
∴x+2x=90,
解得x=30,
∴∠B=2×30°=60°.
∵等腰梯形ABCD中,AB=CD,
又AB=AD,
∴AD=CD,
∴∠ACD=∠CAD=x°.
∵AD∥BC,
∴∠CAD=∠ACB=x°.
∵等腰梯形ABCD中,AB=CD,
∴∠B=∠BCD=2x°.
∵在△ABC中,AB⊥AC,
∴∠ACB+∠B=90°,
∴x+2x=90,
解得x=30,
∴∠B=2×30°=60°.
点评:此题考查了等腰梯形的性质、等腰三角形的性质、平行线的性质以及三角形内角和定理.此题难度适中,注意掌握数形结合思想与方程思想的应用是解此题的关键.

练习册系列答案
相关题目
 如图,a∥b,∠1=(3x+20)°,∠2=(2x+10)°,那么∠3=
如图,a∥b,∠1=(3x+20)°,∠2=(2x+10)°,那么∠3=
 如图,在△ABC中,点D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.
如图,在△ABC中,点D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.
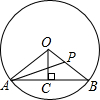 如图,AB是⊙O的弦,OC⊥AB于点C,连接OA、OB.点P是半径OB上的任意一点,连接AP.若OA=5cm,OC=4cm,则AP的长度可能是
如图,AB是⊙O的弦,OC⊥AB于点C,连接OA、OB.点P是半径OB上的任意一点,连接AP.若OA=5cm,OC=4cm,则AP的长度可能是