题目内容
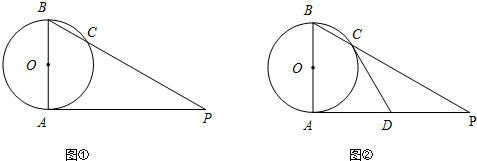
13.已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.(1)如图①,若AB=3$\sqrt{2}$,∠P=30°,求AP的长(结果保留根号);
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
分析 (1)首先根据切线的性质判定∠BAP=90°;然后在直角三角形ABP中利用三角函数的定义求得AP的长度;
(2)连接OC,OD、AC构建全等三角形△OAD≌△OCD,然后利用全等三角形的对应角相等推知∠OAD=∠OCD=90°,即OC⊥CD.
解答 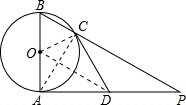 (1)解:∵AB是⊙O的直径,AP是⊙O的切线,
(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,
∴∠BAP=90°;
又∵AB=2,∠P=30°,
∴AP=$\frac{AB}{tan∠P}$$\frac{3\sqrt{2}}{\frac{\sqrt{3}}{3}}$=3$\sqrt{6}$;
(2)证明:如图,连接OC,OD、AC.
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
$\left\{\begin{array}{l}{OA=OC}\\{OD=OD}\\{AD=CD}\end{array}\right.$,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.
点评 本题考查了切线的判定与性质:经过半径的外端且垂直于这条半径的直线是圆的切线;圆的切线垂直于经过切点的半径.也考查了圆周角定理和三角形全等的判定与性质.熟记这些定理是解决问题的关键.

练习册系列答案
相关题目
4.下列图形中,属于棱柱的是( )
| A. |  | B. |  | C. |  | D. |  |
8. 实数a、b在数轴上的位置如图所示,则化简|a+b|+a的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a+b|+a的结果为( )
 实数a、b在数轴上的位置如图所示,则化简|a+b|+a的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a+b|+a的结果为( )| A. | 2a+b | B. | -b | C. | -2a-b | D. | b |
2.“9的算术平方根”记作$\sqrt{9}$,其值是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 9 |
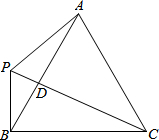 如图,△ABC为等边三角形,P是直线AB左侧一点,连接PA、PB、PC,PC与AB相交于点D,∠BPC=60°.
如图,△ABC为等边三角形,P是直线AB左侧一点,连接PA、PB、PC,PC与AB相交于点D,∠BPC=60°.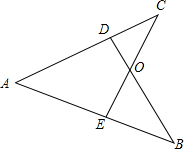 如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC.
如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC.