题目内容
18.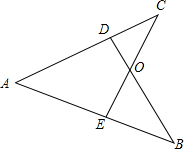 如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC.
如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC.
分析 根据垂直的定义得到∠CDO=∠BEO=90°,推出△CDO≌△BEO,根据全等三角形的性质得到∠C=∠B,OC=OB,证得CE=BD,推出△ABD≌△ACE,根据全等三角形的性质即可得到结论.
解答 证明:∵CE⊥AB于E,BD⊥AC于D,
∴∠CDO=∠BEO=90°,
在△CDO与△BEO中,$\left\{\begin{array}{l}{∠CDO=∠BEO}\\{OD=OE}\\{∠COD=∠BOE}\end{array}\right.$,
∴△CDO≌△BEO,
∴∠C=∠B,OC=OB,
∴OC+OE=OB+OD,
即CE=BD,
在△ABD与△ACE中,$\left\{\begin{array}{l}{∠A=∠A}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE,
∴AB=AC.
点评 本题考查了全等三角形的判定和性质,垂直的定义,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
8.对于抛物线y=5(x+2)2+6,下列说法正确的是( )
| A. | 开口向下,顶点坐标为(2,6) | B. | 开口向下,顶点坐标为(-2,6) | ||
| C. | 开口向上,顶点坐标为(-2,6) | D. | 开口向上,顶点坐标为(-2,-6) |
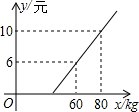 某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票y(元)是行李质量x(kg)的一次函数,其图象如图.求:
某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票y(元)是行李质量x(kg)的一次函数,其图象如图.求: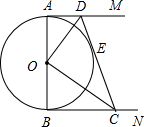 如图,AB是⊙O的直径,AM、BN是⊙O的切线,DE切⊙O于E,交AM于D,交BN于C.
如图,AB是⊙O的直径,AM、BN是⊙O的切线,DE切⊙O于E,交AM于D,交BN于C.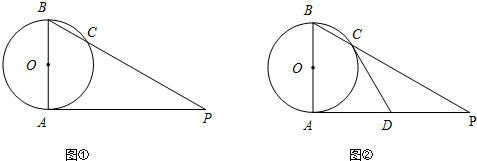
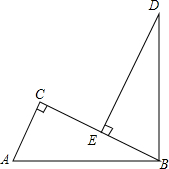 如图,∠ABD=90°,AB=BD,AC⊥BC,DE⊥BC,垂足分别为C、E.求证:AC+CE=DE.
如图,∠ABD=90°,AB=BD,AC⊥BC,DE⊥BC,垂足分别为C、E.求证:AC+CE=DE.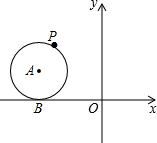 如图,A点的坐标为(-2,1),以A为圆心的⊙A切x轴于点B,P(m,n)为⊙A上的一个动点,请探索n+m的最大值.
如图,A点的坐标为(-2,1),以A为圆心的⊙A切x轴于点B,P(m,n)为⊙A上的一个动点,请探索n+m的最大值.