题目内容
5.平面上不重合的两点确定1条直线,不同三点最多可确定3条直线,若平面上不同的6个点最多可确定15条直线.分析 根据每两个点之间有一条直线,可得n个点最多直线的条数:$\frac{n(n-1)}{2}$.
解答 解:若平面内的不同的6个点最多可确定$\frac{6×(6-1)}{2}$=15条直线,
故答案为:15.
点评 本题考查了直线、射线、线段,熟记n个点最多直线的条数:$\frac{n(n-1)}{2}$是解题关键.

练习册系列答案
相关题目
14.x+2x+3x+4x+5x+…+97x+98x+99x+100x=5050,x的解是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 10 |
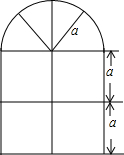 某窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长和半圆的半径均为acm.计算:
某窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长和半圆的半径均为acm.计算: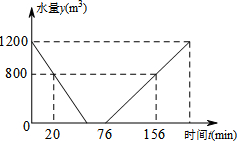 江阴水魔方游泳池常需进行换水清洗,途中的折线表示的是某个游泳池换水清洗过程“排水--清洗--灌水”中水量y(m3)与时间t(min)之间的函数关系式
江阴水魔方游泳池常需进行换水清洗,途中的折线表示的是某个游泳池换水清洗过程“排水--清洗--灌水”中水量y(m3)与时间t(min)之间的函数关系式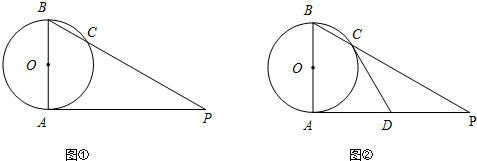
 如图,直角坐标系中.点A的坐标为(1,0),以线段OA为边在第四象限内作等边点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中.点A的坐标为(1,0),以线段OA为边在第四象限内作等边点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.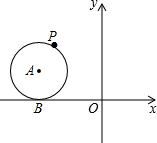 如图,A点的坐标为(-2,1),以A为圆心的⊙A切x轴于点B,P(m,n)为⊙A上的一个动点,请探索n+m的最大值.
如图,A点的坐标为(-2,1),以A为圆心的⊙A切x轴于点B,P(m,n)为⊙A上的一个动点,请探索n+m的最大值. 如图,∠BOC=90°,∠COB与∠AOC之差为60°,试求∠AOB的度数.
如图,∠BOC=90°,∠COB与∠AOC之差为60°,试求∠AOB的度数.