题目内容
1. 如图,AP为⊙O的切线,P为切点,OA交⊙O于点B.若∠A=40°,则∠ABP=115°.
如图,AP为⊙O的切线,P为切点,OA交⊙O于点B.若∠A=40°,则∠ABP=115°.
分析 连结OP,如图,根据切线的性质得∠OPA=90°,则利用互余可计算出∠O=90°-∠A=50°,再利用等腰三角形的性质和三角形内角和可计算出∠OBP=$\frac{1}{2}$(180°-∠O)=70°,然后利用邻补角的定义计算∠ABP的度数.
解答 解:连结OP,如图,
∵AP为⊙O的切线,
∴OP⊥AP,
∴∠OPA=90°,
∴∠O=90°-∠A=90°-40°=50°,
∵OB=OP,
∴∠OBP=∠OPB,
∴∠OBP=$\frac{1}{2}$(180°-∠O)=$\frac{1}{2}$×(180°-50°)=65°,
∴∠ABP=180°-∠OBP=180°-65°=115°.
故答案为115.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
7.某商店按高出成本价的20%卖出一件商品,结果获利a元,那么该商品的成本是( )
| A. | (1+20%)a | B. | (1-20%)a | C. | $\frac{a}{1+20%}$ | D. | $\frac{a}{20%}$ |
16.一个圆心角为36°,半径为20的扇形的面积为( )
| A. | 40π | B. | 20π | C. | 4π | D. | 2π |
13.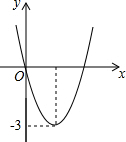 二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的取值范围是( )
二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的取值范围是( )
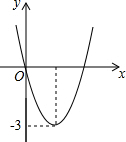 二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的取值范围是( )
二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的取值范围是( )| A. | m≤3 | B. | m≥3 | C. | m≤-3 | D. | m≥-3 |
 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,计算点O到AB与CD边的距离之比.
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,计算点O到AB与CD边的距离之比. 如图,小芳站在地面上A处放风筝,风筝飞到C处时的线长BC为23米,这是测得∠CBD=58°,牵引底端B与地面的距离BA为1.6米,求此时风筝离地面的高度CE.(结果精确到0.1米)
如图,小芳站在地面上A处放风筝,风筝飞到C处时的线长BC为23米,这是测得∠CBD=58°,牵引底端B与地面的距离BA为1.6米,求此时风筝离地面的高度CE.(结果精确到0.1米)