题目内容
13.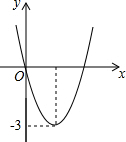 二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的取值范围是( )
二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的取值范围是( )| A. | m≤3 | B. | m≥3 | C. | m≤-3 | D. | m≥-3 |
分析 结合图象可得y≥-3,即ax2+bx≥-3,由ax2+bx+m=0可得ax2+bx=-m,则有-m≥-3,即可解决问题.
解答 方法一:
解:由图可知:y≥-3,即ax2+bx≥-3,
∵ax2+bx+m=0,∴ax2+bx=-m,
∴-m≥-3,
∴m≤3.
方法二:
解:由图象可知,抛物线顶点纵坐标y=$\frac{-{b}^{2}}{4a}$=-3,且a>0,
∴b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2-4am=12a-4am≥0,
即:m≤3,
答案选A.
点评 本题主要考查抛物线与一元二次方程之间的关系、解一元一次不等式等知识,利用数形结合的思想是解决本题的关键.

练习册系列答案
相关题目
18.学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册.设这两年的平均增长率为x,则下列方程正确的是( )
| A. | 5(1+x)=7.2 | B. | 5(1+2x)=7.5 | C. | 5(1+x)2=7.2 | D. | 5(1+x)+5(1+x)2=7.2 |
 已知:如图,AB=AD,BD平分∠ABC,求证:AD∥BC.
已知:如图,AB=AD,BD平分∠ABC,求证:AD∥BC.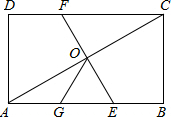 如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E,交AB于E,点G是AE的中点,且∠AOG=30°,则下列结论:(1)DC=3OG;(2)OG=$\frac{1}{2}$BC;(3)四边形AECF为菱形;(4)S△AOE=$\frac{1}{6}$S四边形ABCD.其中正确的个数为( )
如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E,交AB于E,点G是AE的中点,且∠AOG=30°,则下列结论:(1)DC=3OG;(2)OG=$\frac{1}{2}$BC;(3)四边形AECF为菱形;(4)S△AOE=$\frac{1}{6}$S四边形ABCD.其中正确的个数为( ) 如图,AP为⊙O的切线,P为切点,OA交⊙O于点B.若∠A=40°,则∠ABP=115°.
如图,AP为⊙O的切线,P为切点,OA交⊙O于点B.若∠A=40°,则∠ABP=115°. 如图,所给两圆的圆心分别为O1,O2,半径都为3,根据要求完成作图(保留作图痕迹,不写作法).
如图,所给两圆的圆心分别为O1,O2,半径都为3,根据要求完成作图(保留作图痕迹,不写作法). 如图,△ABC∽△ACP,若∠A=75°,∠APC=65°,则∠B的大小为40度.
如图,△ABC∽△ACP,若∠A=75°,∠APC=65°,则∠B的大小为40度.