题目内容
18.某市4所大学(用A、B、C、D表示)各组织部分学生参加“汉语桥”大赛,各学校组织的学生人数绘制成的条形统计图和扇形统计图如图所示.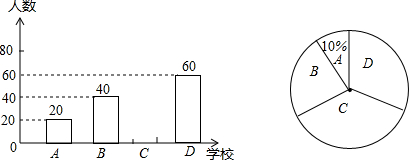
请根据统计图回答下列问题:
(1)将条形统计图补充完整;扇形统计图中C代表的扇形的圆心角为144度;
(2)赛后,大赛组织方从参赛的学生中挑选出2名学生前往西藏的日噶则、那区、山南3个地区(分别用R、N、S表示)宣传汉语,每名学生各自随机选择一个地区进行宣传工作,请用画树状图或列表的方法求出两人恰好都选择了同一地区的概率.
分析 (1)先利用A代表的人数和它所占的百分比计算出样本容量为200,则可计算出C代表的人数为80,然后用360°乘以C代表所占的百分比得到扇形统计图中C代表的扇形的圆心角的度数;最后补全条形统计图;
(2)画树状图展示所有9种等可能的结果数,再找出两人恰好都选择了同一地区的结果数,然后根据概率公式求解.
解答 解:(1)20÷10%=200,
所以样本容量为200,
所以C代表的人数为200-20-40-60=80(人),
所以扇形统计图中C代表的扇形的圆心角的度数为360°×$\frac{80}{200}$=144°;
条形统计图补充完整为:
故答案为144;
(2)画树状图为:
共有9种等可能的结果数,其中两人恰好都选择了同一地区的结果数为3,
所以两人恰好都选择了同一地区的概率=$\frac{3}{9}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.也考查了统计图.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
7.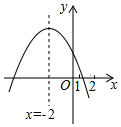 如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )
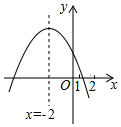 如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.已知关于x的一元二次方程x2-4x+a=0有两个不相等的实数根,则a的取值范围是( )
| A. | a>4 | B. | a<4 | C. | a≤4 | D. | a<4,且a≠0 |
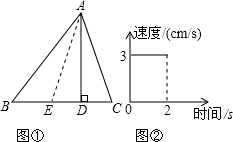 如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②
如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②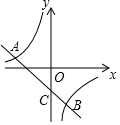 如图:一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(-3,1)、B(1,n)两点.
如图:一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(-3,1)、B(1,n)两点.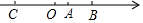 如图,已知A,B,C是数轴上三点,O为原点,点A点B在原点的右侧,点C在原点的左侧,点A表示的数为m,若关于x 的多项式-x3+12x2-3mx2-2x+4不含x2,且AB=6,AC=24.
如图,已知A,B,C是数轴上三点,O为原点,点A点B在原点的右侧,点C在原点的左侧,点A表示的数为m,若关于x 的多项式-x3+12x2-3mx2-2x+4不含x2,且AB=6,AC=24.