题目内容
7.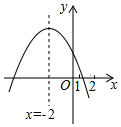 如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据函数图象可得a、b、c的符号从而可以判断①是否正确;②由对称轴为直线x=-2,可判断②是否正确;③由对称轴为直线x=-2,当x=-3时,判断9a-3b+c的符号;④由②③可知,把b=4a代入9a-3b+c>0得-3a+c>0.
解答 解:∵抛物线开口向下,a<0,抛物线与y轴正半轴相交,c>0,对称轴在y轴左侧,b<0,
∴abc>0,故①错误;
∵抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,
∴-$\frac{b}{2a}$=-2,
∴b=4a,
∴4a-b=0,故②错误;
当x=-3时,y=9a-3b+c<0,③正确;
由②③可知,把b=4a代入9a-3b+c>0得-3a+c>0,故④错误;
故选A.
点评 本题主要考查抛物线的性质.此题考查了数形结合思想,解题时要注意数形结合.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
12. 如图是由几个相同的小正方体摆成的组合图形,其主视图为( )
如图是由几个相同的小正方体摆成的组合图形,其主视图为( )
 如图是由几个相同的小正方体摆成的组合图形,其主视图为( )
如图是由几个相同的小正方体摆成的组合图形,其主视图为( )| A. |  | B. |  | C. |  | D. |  |
19.-$\frac{1}{5}$的倒数是( )
| A. | -5 | B. | 5 | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
16.下列运算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | (a+b)2=a2+b2 | C. | (a2+5)0=1 | D. | (-a2)3=a6 |
17.下列说法不正确的是( )
| A. | 调查一架“歼20”隐形战机各零部件的质量,应采用抽样调查 | |
| B. | 一组数据2,2,3,3,3,4的众数是3 | |
| C. | 如果x1与x2的平均数是4,那么x1+1与x2+5的平均数是7 | |
| D. | 一组数据1,2,3,4,5的方差是2,那么数据11,12,13,14,15的方差也是2 |
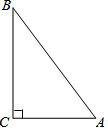 已知在△ABC中,∠ACB=90°,AB=10,cosA=$\frac{3}{5}$(如图),将△ABC绕着点C旋转,点A、B的对应点分别记为A′、B′,A′B′与边AB相交于点E.如果A′B′⊥AC,那么线段B′E的长为$\frac{24}{5}$.
已知在△ABC中,∠ACB=90°,AB=10,cosA=$\frac{3}{5}$(如图),将△ABC绕着点C旋转,点A、B的对应点分别记为A′、B′,A′B′与边AB相交于点E.如果A′B′⊥AC,那么线段B′E的长为$\frac{24}{5}$.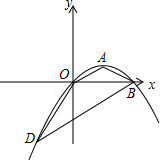 已知,抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(s,t)(s≠0).
已知,抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(s,t)(s≠0).