题目内容
3.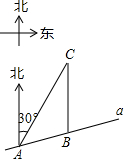 如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量,B位于A的北偏东75°方向,C位于B的正北方向,C位于A的北偏东30°方向,AB=8km.
如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量,B位于A的北偏东75°方向,C位于B的正北方向,C位于A的北偏东30°方向,AB=8km.(1)求景点B与C的距离;
(2)为方便游客到景点游玩,景区管委会准备由景点C向公路a修一条距离最短的公路,不考虑其它因素,求出这条公路的长.(本题结果保留根号)
分析 (1)首先过点B作BD⊥AC于点D,由在Rt△ADB中,∠ADB=90°,∠DAB=45°,可求得BD的长,然后由在Rt△CDB中,∠CDB=90°,∠DCB=30°,求得BC的长;
(2)首先过点C作CE⊥AB于点E,继而求得AD,CD与AC的长,然后在Rt△CAE中,求得答案.
解答 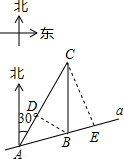 解:(1)如图,过点B作BD⊥AC于点D.
解:(1)如图,过点B作BD⊥AC于点D.
在Rt△ADB中,∠ADB=90°,∠DAB=45°,
∴$sin{45°}=\frac{BD}{8}=\frac{{\sqrt{2}}}{2}$.
∴BD=$4\sqrt{2}$,
在Rt△CDB中,∠CDB=90°,∠DCB=30°,
∴$sin{30°}=\frac{{4\sqrt{2}}}{BC}=\frac{1}{2}$.
∴BC=$8\sqrt{2}$km;
(2)过点C作CE⊥AB于点E.
在(1)中可求出AD=$4\sqrt{2}$,CD=$4\sqrt{6}$,则AC=$4\sqrt{2}$+$4\sqrt{6}$,
在Rt△CAE中,sin∠CAE=$\frac{CE}{AC}=\frac{{\sqrt{2}}}{2}$,
∴代入求出CE=(4+$4\sqrt{3}$)km.
点评 此题考查了方向角问题.注意准确构造直角三角形是解此题的关键.

练习册系列答案
相关题目
13.下列各图中,能够由∠1=∠2得到AB∥CD的是( )
| A. | 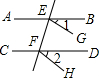 | B. | 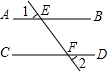 | C. | 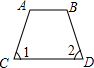 | D. | 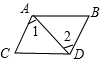 |
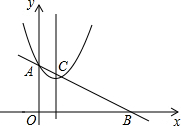 如图,在平面直角坐标系中,抛物线y=x2-2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为(1,$\frac{3}{2}$).
如图,在平面直角坐标系中,抛物线y=x2-2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为(1,$\frac{3}{2}$).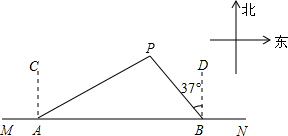 如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).
如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).