题目内容
20. 如图,抛物线y=ax2+bx+c请根据图象写出该图象两条性质:①开口方向向下;②对称轴x=1,当x>1时,y随着x的增大而减小,当x<1时,y随着x的增大而增大..
如图,抛物线y=ax2+bx+c请根据图象写出该图象两条性质:①开口方向向下;②对称轴x=1,当x>1时,y随着x的增大而减小,当x<1时,y随着x的增大而增大..
分析 结合图象,根据开口方向、对称轴以及增减性得出答案即可.
解答  解:如图,抛物线y=ax2+bx+c的性质:
解:如图,抛物线y=ax2+bx+c的性质:
①开口方向向下;
②对称轴x=1,当x>1时,y随着x的增大而减小,当x<1时,y随着x的增大而增大.
故答案为:①开口方向向下;②对称轴x=1,当x>1时,y随着x的增大而减小,当x<1时,y随着x的增大而增大.
点评 此题考查二次函数的图象与性质,结合图象,正确判定开口方向、对称轴以及增减性解决问题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
10.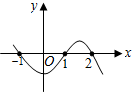 已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )
已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )
 已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )
已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )| A. | x<0 | B. | x<-1或1<x<2 | C. | -1<x<1或x>2 | D. | x>-1 |
8.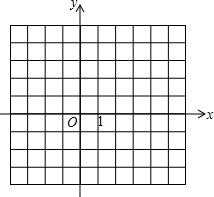 在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
(1)求这个二次函数的解析式及m的值;
(2)在平面直角坐标系中,用描点法画出这个二次函数的图象(不用列表);
(3)当y<3时,则x的取值范围是0<x<4.
 在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | m | … |
(2)在平面直角坐标系中,用描点法画出这个二次函数的图象(不用列表);
(3)当y<3时,则x的取值范围是0<x<4.
15.等腰三角形一腰上的高与另一腰的夹角是28°,则顶角是( )
| A. | 28° | B. | 118° | C. | 62° | D. | 62°或118° |
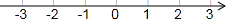 (1)解不等式2(x+1)-1≥3x+2.并把它的解集在数轴上表示出来.
(1)解不等式2(x+1)-1≥3x+2.并把它的解集在数轴上表示出来. 解不等式组:$\left\{\begin{array}{l}{6m+3<m-2}\\{3+m≥3(m-1)}\end{array}\right.$,并把它的解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}{6m+3<m-2}\\{3+m≥3(m-1)}\end{array}\right.$,并把它的解集在数轴上表示出来.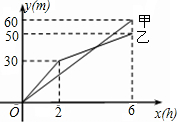 甲、乙两个工程队分别同时开始挖两段河渠,所挖河渠的长度与挖掘时间之间的关系如图所示,请根据图象所提供的信息解答下列问题:
甲、乙两个工程队分别同时开始挖两段河渠,所挖河渠的长度与挖掘时间之间的关系如图所示,请根据图象所提供的信息解答下列问题: