题目内容
5.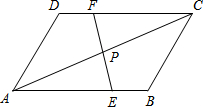 如图,?ABCD中,点E、F分别在AB、CD上,且BE=DF,EF与AC相交于点P,求证:PA=PC.
如图,?ABCD中,点E、F分别在AB、CD上,且BE=DF,EF与AC相交于点P,求证:PA=PC.
分析 首先根据平行四边形的性质可得AB=CD,AB∥CD,进而可得∠AEP=∠CFP,AE=CF,然后证明△AEP≌△CFP,可得PA=PC.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠AEP=∠CFP,
∵BE=DF,
∴AB-BE=CD-DF,即AE=CF,
在△AEP和△CFP中,
$\left\{\begin{array}{l}{∠AEP=∠CFP}\\{∠APE=∠CPF}\\{AE=CF}\end{array}\right.$,
∴△AEP≌△CFP(AAS),
∴PA=PC.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形对边平行且相等.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
16.一个不透明的袋中装有红、白、黄3种颜色的若干个小球,它们除颜色外完全相同.每次从袋中摸出1个球,记下颜色后放回搅匀再摸.摸球实验中,统计得到下表中的数据:
由此可以估计摸到黄球的概率约为0.4(精确到0.1).
| 摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
| 出现白球的频数 | 1 | 4 | 16 | 36 | 52 | 61 | 75 | 85 | 123 | 151 |
13.下列说法正确的是 ( )
| A. | 为了了解某中学800名学生的视力情况,从中随机抽取了50名学生进行调查,在此次调查中,样本容量为50名学生的视力 | |
| B. | 若一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖 | |
| C. | 了解无锡市每天的流动人口数,采用抽查方式 | |
| D. | “掷一枚硬币,正面朝上”是必然事件 |
14.已知a,b,c是三角形的三边,那么代数式(a-b)2-c2的值( )
| A. | 大于零 | B. | 小于零 | C. | 等于零 | D. | 不能确定 |