题目内容
6.观察下表多项式分解因式的特征,并回答问题.| 1 | 2 | 3 | 4 |
| 多项式 | 常数项 | 一次项系数 | 分解因式 |
| x2+6x+8 | 8=2×4 | 6=2+4 | x2+6x+8=(x+2)(x+4) |
| x2-6x+8 | 8=(-2)×(-4) | -6=(-2)+(-4) | x2-6x+8=(x-2)(x-4) |
| x2+2x-8 | -8=4×(-2) | 2=4+(-2) | x2+2x-8=(x+4)(x-2) |
(1)分解因式:x2-4x-60;
(2)若x2+px-60可分解为两个一次因式的积,则整数p的值有12个.
分析 (1)根据常数项与一次项系数的关系进行因式分解;
(2)把-60分解为两个整数的积的形式,p等于这两个整数的和.
解答 解:(1)x2-4x-60=(x-10)(x+6);
(2)-60=(±1)×60=(±2)×30=(±3)×20=(±4)×15=(±5)×12=(±6)×10,
所以p=(±1)+60或(±2)+30=或(±3)+20或(±4)+15或(±5)+12或(±6)+10,
则整数p的值有12个.
故答案是:12.
点评 本题考查了十字相乘法分解因式,对常数项的不同分解是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
16.一个不透明的袋中装有红、白、黄3种颜色的若干个小球,它们除颜色外完全相同.每次从袋中摸出1个球,记下颜色后放回搅匀再摸.摸球实验中,统计得到下表中的数据:
由此可以估计摸到黄球的概率约为0.4(精确到0.1).
| 摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
| 出现白球的频数 | 1 | 4 | 16 | 36 | 52 | 61 | 75 | 85 | 123 | 151 |
14.已知a,b,c是三角形的三边,那么代数式(a-b)2-c2的值( )
| A. | 大于零 | B. | 小于零 | C. | 等于零 | D. | 不能确定 |
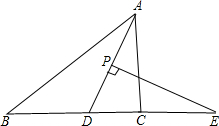 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.