题目内容
9.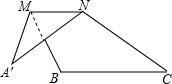 如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A=30°,∠B=115°,则∠A′NC=110°.
如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A=30°,∠B=115°,则∠A′NC=110°.
分析 先利用内角和定理求∠C,根据三角形的中位线定理可知MN∥BC,由平行线的性质可求∠A′NM、∠CNM,再利用角的和差关系求∠A′NC.
解答 解:∵∠A=30°,∠B=115°,
∴∠C=180°-∠A-∠B=180°-30°-115°=35°,
∵MN是三角形的中位线,
∴MN∥BC,
∴∠A′NM=∠C=35°,∠CNM=180°-∠C=180°-35°=145°,
∴∠A′NC=∠CNM-∠A′NM=145°-35°=110°.
故答案为:110.
点评 本题考查的是三角形中位线定理、翻折变换,熟知图形翻折不变性的性质是解答此题的关键.

练习册系列答案
相关题目
14.已知a,b,c是三角形的三边,那么代数式(a-b)2-c2的值( )
| A. | 大于零 | B. | 小于零 | C. | 等于零 | D. | 不能确定 |
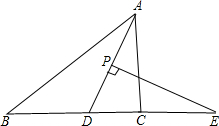 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E. 已知:如图,点B,F,C,E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:∠B=∠E.
已知:如图,点B,F,C,E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:∠B=∠E.