题目内容
20. 已知a,b两数在数轴上的位置如图所示,则化简代数式|a+b|-|a-1|-|b+2|的结果是( )
已知a,b两数在数轴上的位置如图所示,则化简代数式|a+b|-|a-1|-|b+2|的结果是( )| A. | 1 | B. | 2b+3 | C. | 2a-3 | D. | -1 |
分析 根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,即可得到结果.
解答 解:由数轴可知-2<b<-1,1<a<2,且|a|>|b|,
所以a+b>0,a-1>0,b+2>0,
则|a+b|-|a-1|-|b+2|=a+b-(a-1)-(b+2)=a+b-a+1-b-2=-1.
故选D.
点评 此题考查了整式的加减,数轴,以及绝对值,判断出绝对值里边式子的正负是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.计算5+(-22)的结果是( )
| A. | 27 | B. | 17 | C. | -17 | D. | -27 |
8.下列计算正确的是( )
| A. | a3•a2=a6 | B. | 3a(a-2b)=3a2-2ab | C. | a4÷a5=a-1 | D. | 30=0 |
15.单项式a2b的系数和次数分别是( )
| A. | 1,2 | B. | 2,1 | C. | 1,3 | D. | 0,3 |
5.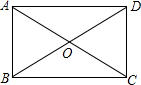 如图,在矩形ABCD中,AB=2,∠AOB=60°,则OB的长为( )
如图,在矩形ABCD中,AB=2,∠AOB=60°,则OB的长为( )
 如图,在矩形ABCD中,AB=2,∠AOB=60°,则OB的长为( )
如图,在矩形ABCD中,AB=2,∠AOB=60°,则OB的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.如果a>b,那么下列结论一定正确的是( )
| A. | a-3<b-3 | B. | 1+a>1+b | C. | -3a>-3b | D. | $\frac{a}{3}$<$\frac{b}{3}$ |
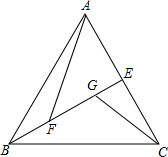 如图,△ABC是等边三角形,BE⊥AC于E,点F、G在BE上(BF<BG),连接AF,CG,CG2=GF•GB,
如图,△ABC是等边三角形,BE⊥AC于E,点F、G在BE上(BF<BG),连接AF,CG,CG2=GF•GB,