题目内容
3.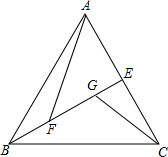 如图,△ABC是等边三角形,BE⊥AC于E,点F、G在BE上(BF<BG),连接AF,CG,CG2=GF•GB,
如图,△ABC是等边三角形,BE⊥AC于E,点F、G在BE上(BF<BG),连接AF,CG,CG2=GF•GB,(1)求证:∠AFE=∠BCG;
(2)过点F作直线CG的垂线,垂足为H,M为AB的中点,连接MH,探究MH与BF之间的数量关系,并证明你的结论.
分析 (1)如图1,连结CF,由CG2=GF•GB,加上∠CGF=∠BGC,则可判断△CGF∽△BGC,则∠GFC=∠BCG,再根据等边三角形的性质得∠AFE=∠GFC,所以∠AFE=∠BCG;
(2)连结ME,HE,CM,如图2,根据等边三角形的性质得∠2=∠EBC=∠BCM=30°,再利用△CGF∽△BGC得到∠GCF=∠GBC=30°,则∠1=∠MCH,接着证明H、E点在以FC为直径的圆上,理由圆周角定理得到∠3=∠HCF=30°,于是可判断HE∥BC,而ME∥BC,所以点H在ME上,即有MH∥BC,所以∠HMC=∠MCB=30°,∠2=∠HMC,于是可得到△ABF∽△CMH,利用相似比得BF:MH=AB:CM,由于CM=$\sqrt{3}$BM=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$AB,所以MH=$\frac{\sqrt{3}}{2}$BF.
解答 (1)证明:如图1,连结CF, ∵CG2=GF•GB,即$\frac{CG}{GB}$=$\frac{GF}{GC}$,
∵CG2=GF•GB,即$\frac{CG}{GB}$=$\frac{GF}{GC}$,
而∠CGF=∠BGC,
∴△CGF∽△BGC,
∴∠GFC=∠BCG,
∵△ABC是等边三角形,BE⊥AC,
∴AE=CE,
∴FE平分∠AFC,
∴∠AFE=∠GFC,
∴∠AFE=∠BCG;
(2)解:MH=$\frac{\sqrt{3}}{2}$BF.
理由如下:连结ME,HE,CM,如图2,
∵△ABC是等边三角形,M点为中点,BE⊥AC,
∴∠2=∠EBC=∠BCM=30°,
∵△CGF∽△BGC,
∴∠GCF=∠GBC=30°,
∴∠1=∠MCH,
∵FH⊥CG,
∴∠FGC=90°,
而∠FEC=90°,
∴H、E点在以FC为直径的圆上,
∴∠3=∠HCF=30°,
∴HE∥BC,
∵ME为△ABC的中位线,
∴ME∥BC,
∴点H在ME上,
∴MH∥BC,
∴∠HMC=∠MCB=30°,
∴∠2=∠HMC,
∴△ABF∽△CMH,
∴BF:MH=AB:CM,
在Rt△BCM中,BM=$\frac{1}{2}$BC,
CM=$\sqrt{3}$BM=$\frac{\sqrt{3}}{2}$BC,
∴CM=$\frac{\sqrt{3}}{2}$AB,
∴MH=$\frac{\sqrt{3}}{2}$BF.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.在利用相似三角形的性质时,注意通过相似比计算相应线段的长或对应角线段.解决本题的关键是构建含BF和MH的两三角形相似,同时熟练掌握等边三角形的性质.

 阅读快车系列答案
阅读快车系列答案| A. | y=(x-1)2+2 | B. | y=(x+1)2-2 | C. | y=(x-2)2-1 | D. | y=(x-1)2-2 |
 如图,在△ABC中,∠ADE=∠B,DE:BC=2:3,则下列结论正确的是( )
如图,在△ABC中,∠ADE=∠B,DE:BC=2:3,则下列结论正确的是( )| A. | AD:AB=2:3 | B. | AE:AC=2:5 | C. | AD:DB=2:3 | D. | CE:AE=3:2 |
 已知a,b两数在数轴上的位置如图所示,则化简代数式|a+b|-|a-1|-|b+2|的结果是( )
已知a,b两数在数轴上的位置如图所示,则化简代数式|a+b|-|a-1|-|b+2|的结果是( )| A. | 1 | B. | 2b+3 | C. | 2a-3 | D. | -1 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| A. | (x-30)[600+10(x-40)]=10 000 | B. | (x-30)[600-10(x-40)]=10 000 | ||
| C. | (x-40)[600-10(x-40)]=10 000 | D. | (x-40)[600+10(x-40)]=10 000 |
| A. | (3,-1) | B. | (1,3) | C. | (-3,1) | D. | (-1,-3) |
 已知△ABC,请你用两种不同的方法把它分成面积之比为1:2:3的三个三角形.
已知△ABC,请你用两种不同的方法把它分成面积之比为1:2:3的三个三角形.